Question

What is the direct variation equation that goes through the point \[\left( 2,5 \right)\]?

Answer 1

Hint: In this problem we have to find the direct variation equation which goes through the given point \[\left( 2,5 \right)\]. We know that the ratio between two variables that remains constant is said to be direct variation. As per direct variation if x increases y also increases. This is known as direction variation. Whereas direction variation between two variables x and y can be denoted by, \[y\propto x\]. Where \[\propto \] means proportional to. Therefore y is proportional to x, this denotes where x increases y also increases. Instead of the proportional (\[\propto \]) symbol a constant can be added. Let the constant be k, therefore the direct variation equation is

Complete step-by-step solution:
We know that the direct variation equation is,
\[\Rightarrow y=kx\] ……… (1)
Here we are provided with a point \[\left( 2,5 \right)\]where,
\[\Rightarrow \left( x,y \right)=\left( 2,5 \right)\]
Therefore
\[\begin{align}
  & \Rightarrow x=2 \\
 & \Rightarrow y=5 \\
\end{align}\]
We can now substituting these points in the equation number (1) we get,
\[\Rightarrow 5=k2\]
 Where the value of k is,
\[\Rightarrow k=\dfrac{5}{2}\] ……… (2)
Now we can substituting the value of the constant k in direct variation equation (1),
\[\Rightarrow y=\dfrac{5}{2}x\]

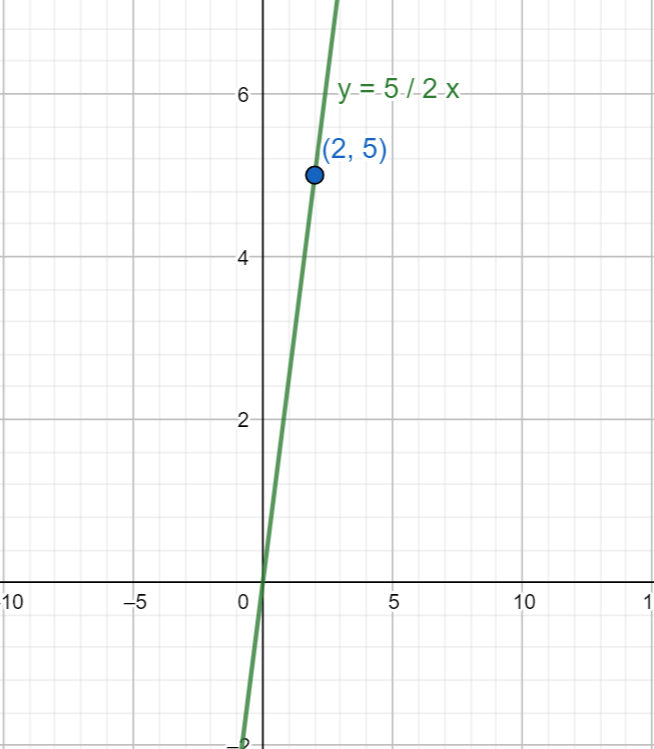
Therefore, the direct variation equation that goes through the point \[\left( 2,5 \right)\] is \[y=\dfrac{5}{2}x\]

Note: A direct variation is the ratio between the two variables which remains constant. According to the direction when x increases y also increases similarly when x decreases y also decreases. Opposite to direct variation there is another one known as inverse or indirect variation. In indirect variation one variable will be constant and the other will be the inverse of the constant one. It is important to read the given question carefully whether it is given direct variation or indirect variation.