Questions & Answers
Question
AnswersHow many diagonals does each of the following have?
$\left( a \right)$ A convex quadrilateral
$\left( b \right)$ A regular hexagon
$\left( c \right)$ A triangle.
Answer
Verified147.6k+ views
Hint: In this question we have to find the number of diagonals for the specific given options, a diagonal is a line segment joining any two opposite corners of a polygon whether it is a square, rhombus, regular hexagon etc. The general formula for the number of diagonals of n-sided polygon is $\dfrac{{n\left( {n - 3} \right)}}{2}$. Use this concept to get the answer.
Complete step-by-step answer:
The general formula for number of diagonals (d) in any figure is
(n-3) multiply by the number of vertices and divide by 2.
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2}$
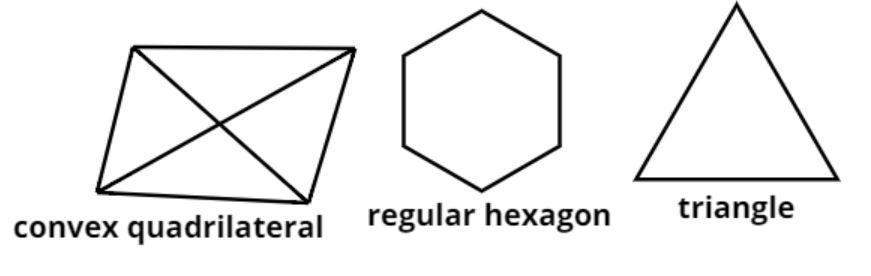
$\left( a \right)$ A convex quadrilateral
As we know in a convex quadrilateral there are four sides (see figure)
$ \Rightarrow n = 2$
Therefore number of diagonals in a convex quadrilateral is
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2} = \dfrac{{4\left( {4 - 3} \right)}}{2} = \dfrac{4}{2} = 2$
$\left( b \right)$ A regular hexagon
As we know in a convex quadrilateral there are six sides (see figure)
$ \Rightarrow n = 6$
Therefore number of diagonals in a convex quadrilateral is
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2} = \dfrac{{6\left( {6 - 3} \right)}}{2} = \dfrac{{6 \times 3}}{2} = 9$
$\left( c \right)$ A triangle.
As we know in a convex quadrilateral there are three sides (see figure)
$ \Rightarrow n = 3$
Therefore number of diagonals in a convex quadrilateral is
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2} = \dfrac{{3\left( {3 - 3} \right)}}{2} = \dfrac{0}{2} = 0$
So, these are the required diagonals in the following figures.
Note: Whenever we face such types of problems the key concept is the basic understanding of the definition of diagonal of a polygon. The gist of direct formula for diagonal of a n-sided polygon will eventually help you in getting the right track to reach the answer accurately.
Complete step-by-step answer:
The general formula for number of diagonals (d) in any figure is
(n-3) multiply by the number of vertices and divide by 2.
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2}$
$\left( a \right)$ A convex quadrilateral
As we know in a convex quadrilateral there are four sides (see figure)
$ \Rightarrow n = 2$
Therefore number of diagonals in a convex quadrilateral is
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2} = \dfrac{{4\left( {4 - 3} \right)}}{2} = \dfrac{4}{2} = 2$
$\left( b \right)$ A regular hexagon
As we know in a convex quadrilateral there are six sides (see figure)
$ \Rightarrow n = 6$
Therefore number of diagonals in a convex quadrilateral is
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2} = \dfrac{{6\left( {6 - 3} \right)}}{2} = \dfrac{{6 \times 3}}{2} = 9$
$\left( c \right)$ A triangle.
As we know in a convex quadrilateral there are three sides (see figure)
$ \Rightarrow n = 3$
Therefore number of diagonals in a convex quadrilateral is
$ \Rightarrow d = \dfrac{{n\left( {n - 3} \right)}}{2} = \dfrac{{3\left( {3 - 3} \right)}}{2} = \dfrac{0}{2} = 0$
So, these are the required diagonals in the following figures.
Note: Whenever we face such types of problems the key concept is the basic understanding of the definition of diagonal of a polygon. The gist of direct formula for diagonal of a n-sided polygon will eventually help you in getting the right track to reach the answer accurately.