Question

Diagonals \[AC\] and $BD$ of a trapezium $ABCD$ with $AB\parallel DC$ intersect each other at the point $O$. Using a similarity criterion for two triangles, show that $\dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}$

Answer 1

Hint:In this question, they give the relation in the trapezium. So, here we have to use the similarity criterion for two triangles to prove the requirement result. We know that the corresponding sides of the two triangles are in proportion when the two triangles are similar. So in order to prove $\dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}$ we need to prove that the two triangles are congruent.

Complete step-by-step answer:

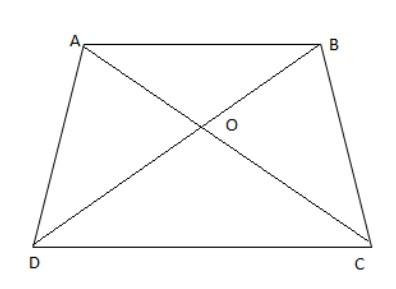
It is mentioned as given in the question that $ABCD$ is a trapezium whose diagonals $AC$and $BD$intersect each other at the point$O$ and $AB\parallel CD$.
In $\Delta OAB$ and $\Delta OCD$, we can see that $\angle AOB$ and $\angle DOC$ are vertically opposite angles so they are equal.
$ \Rightarrow \angle AOB = \angle DOC$
As it is given in the question $AB\parallel DC$ with $BD$ as transversal, so alternate angles will be equal
$ \Rightarrow \angle ABO = \angle CDO$
Again, since $AB\parallel DC$ with $AC$ as transversal, alternate angles will be equal
$ \Rightarrow \angle BAO = \angle OCD$
Hence, it can be said that $\Delta OAB$ and $\Delta OCD$ are similar as it satisfies the condition of congruency because all the corresponding angles of the two triangles are equal.
Therefore we can write, $\Delta OAB \sim \Delta OCD$.
Since, both the triangles are similar, their corresponding sides will be in proportion
So, $\dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}$
Thus it is proved that $\dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}$

Note:There are four conditions for testing the similarity of two triangles.Firstly if all the angles of both the triangles are equal which is known as AAA, Secondly if all the corresponding sides of the triangle are equal which is regarded as SSS, Thirdly if two corresponding sides of the triangle and the angle included between them are equal which is known as SAS and Fourthly if two angles of both the triangles are equal then also the two triangles are similar which is known as AA. So if the two triangles satisfy anyone of the above condition then the two triangles will be treated as similar triangles.