Question

Determine whether the points are collinear. $P =( - 2,3)$,$B = (1,2)$, $C = \left( {4,1} \right)$

Answer 1

Hint: To prove that the points are collinear we have to prove that they are on the same line. Three cases are possible in such a situation

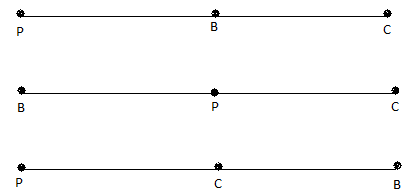
Case1: $PB + BC = PC$
Case 2: $BP + PC = BC$
Case 3: $PC + CB = PB$
If the given points satisfied any one of the above cases then they are collinear otherwise it is not a collinear.

Formula used: Distance between the two points formula, that is $\sqrt {({x_2} - {x_1})_{}^2 + ({y_2} - {y_1})_{}^2} $

Complete step-by-step answer:
It is given that the points are, $P = ( - 2,3)$,$B = (1,2)$and $C = \left( {4,1} \right)$
Here we find out the case 1: $PB + BC = PC$

We have to find out the length of $PB$ by applying the distance formula that is $\sqrt {({x_2} - {x_1})_{}^2 + ({y_2} - {y_1})_{}^2} $
Here, \[\left( {{x_1},{y_1}} \right) = \left( { - 2,3} \right)\]
\[\left( {{x_2},{y_2}} \right) = \left( {1,2} \right)\]
Therefore $PB = \sqrt {(1 + 2)_{}^2 + (2 - 3)_{}^2} = \sqrt {9 + 1} = \sqrt {10} $
Now we have to find out the value of $BC$
Here, \[\left( {{x_1},{y_1}} \right) = \left( {1,2} \right)\]
\[\left( {{x_2},{y_2}} \right) = \left( {4,1} \right)\]
Therefore, the given point are taken by using the distance formula for we get,
$BC$$ = \sqrt {(4 - 1)_{}^2 + (1 - 2)_{}^2} = \sqrt {9 + 1} = \sqrt {10} $
Now we have to find out the value of $PC$
Here, \[\left( {{x_1},{y_1}} \right) = \left( { - 2,3} \right)\]
\[\left( {{x_2},{y_2}} \right) = \left( {4,1} \right)\]
Therefore, the given points are taken by using the distance formula we get, $PC = \sqrt {\{ 4 - ( - 2)\} _{}^2 + (1 - 3)_{}^2} = \sqrt {36 + 4} = \sqrt {40} = 2\sqrt {10} $
Now we have to check the condition when we apply $PB + BC = PC$ we get
$\sqrt {10} + \sqrt {10} = 2\sqrt {10} $
Hence it satisfies the case 1 condition.

Therefore, the given points are collinear.

Note: Two or more points can be regarded as collinear when the points lie on the same line.
If they are present on different lines they are known as non-collinear points. For being collinear they need to satisfy any of the above conditions.
Beside the above method which is by applying distance formula we can also solve the question by applying other methods like by applying area of triangle formula of vertices and if the area of the triangle becomes zero then the points are collinear.
We can also solve the problem by applying the concept of equation of line.