Question

Determine whether the following equations are consistent or inconsistent.
2x+y-6=0
4x-2y-4=0

Answer 1

Hint: Let ax+by+c= 0,AX+BY+C=0 be the given system of equations. Then the given system is consistent if $\dfrac{a}{A}\ne \dfrac{b}{B}$ or $\dfrac{a}{A}=\dfrac{b}{B}=\dfrac{c}{C}$ and the given system is inconsistent if $\dfrac{a}{A}=\dfrac{b}{B}\ne \dfrac{c}{C}$. Use the above result to determine whether the above system is inconsistent.


Complete step-by-step solution -
Consistent and inconsistent system of equations:
A system of equations is said to be consistent if there exists at least one solution of the system.
If the system has no solution, the system is said to be inconsistent.
e.g. the system of equations x+y = 2 is consistent , whereas x = 2+x is inconsistent.

Consistency and inconsistency of the system of linear equations in two variables can be found using the following property:
Let ax+by+c= 0,AX+BY+C=0 be the given system of equations. Then the given system is consistent if $\dfrac{a}{A}\ne \dfrac{b}{B}$ or $\dfrac{a}{A}=\dfrac{b}{B}=\dfrac{c}{C}$ and the given system is inconsistent if $\dfrac{a}{A}=\dfrac{b}{B}\ne \dfrac{c}{C}$.
Using this property we have a = 2, b = 1 , c=-6 , A = 4, B = -2, and C = -4.
Hence we have $\dfrac{a}{A}=\dfrac{2}{4}=\dfrac{1}{2},\dfrac{b}{B}=\dfrac{1}{-2}=-\dfrac{1}{2}$
Hence we have $\dfrac{a}{A}\ne \dfrac{b}{B}$.
Hence the given system of equations is consistent.

Notes: We can also solve the above question graphically. If the lines intersect or overlap then the system is consistent. If the lines are parallel to each other, then the system is inconsistent.

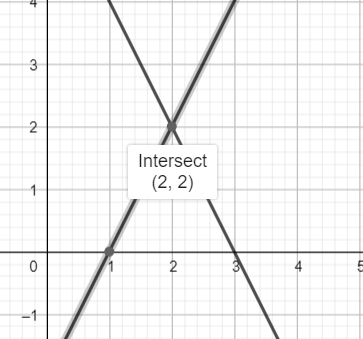
As is evident from the graph, the lines intersect, and hence the given system is consistent.
The consistency of linear equations in three or more variables is determined by finding the rank of the Augmented matrix and comparing it with the rank of matrix A.
If rank(A) = rank(Augmented matrix) then the system is consistent.
Otherwise, the system is inconsistent.