Question

How do you determine whether each equation is a linear equation: $xy = 6$?

Answer 1

Hint: In this question, we have to determine whether a given equation is a linear equation. For this, we have to make a given equation in the form of slope intercept form of a line. It can be done by first dividing both sides of the equation by $x$. Then, check if our equation has exponents. If it has exponents, it is nonlinear.
The Slope Intercept Form of a Line:
The equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.

Complete step by step solution:
We know that the slope intercept form of a line is the equation of a line with slope $m$ and making an intercept $c$ on $y$-axis is $y = mx + c$.
Given equation is $xy = 6$
So, we have to make a given equation in the form of $y = mx + c$, the equation of a line with slope $m$ and making an intercept $c$ on $y$-axis. Then, check if our equation has exponents. If it has exponents, it is nonlinear.
First, divide both sides of the equation by $x$.
$ \Rightarrow y = \dfrac{6}{x}$
Since, our equation has exponents, it is a nonlinear equation.

Hence, $xy = 6$ is a nonlinear equation.

Note: We can also check whether a given equation is a linear equation by plotting the equation.
Then, determine whether the graph is straight line or curved.
If the line is straight, the equation is linear. If it is curved, it is a nonlinear equation.
Graph of $xy = 6$:

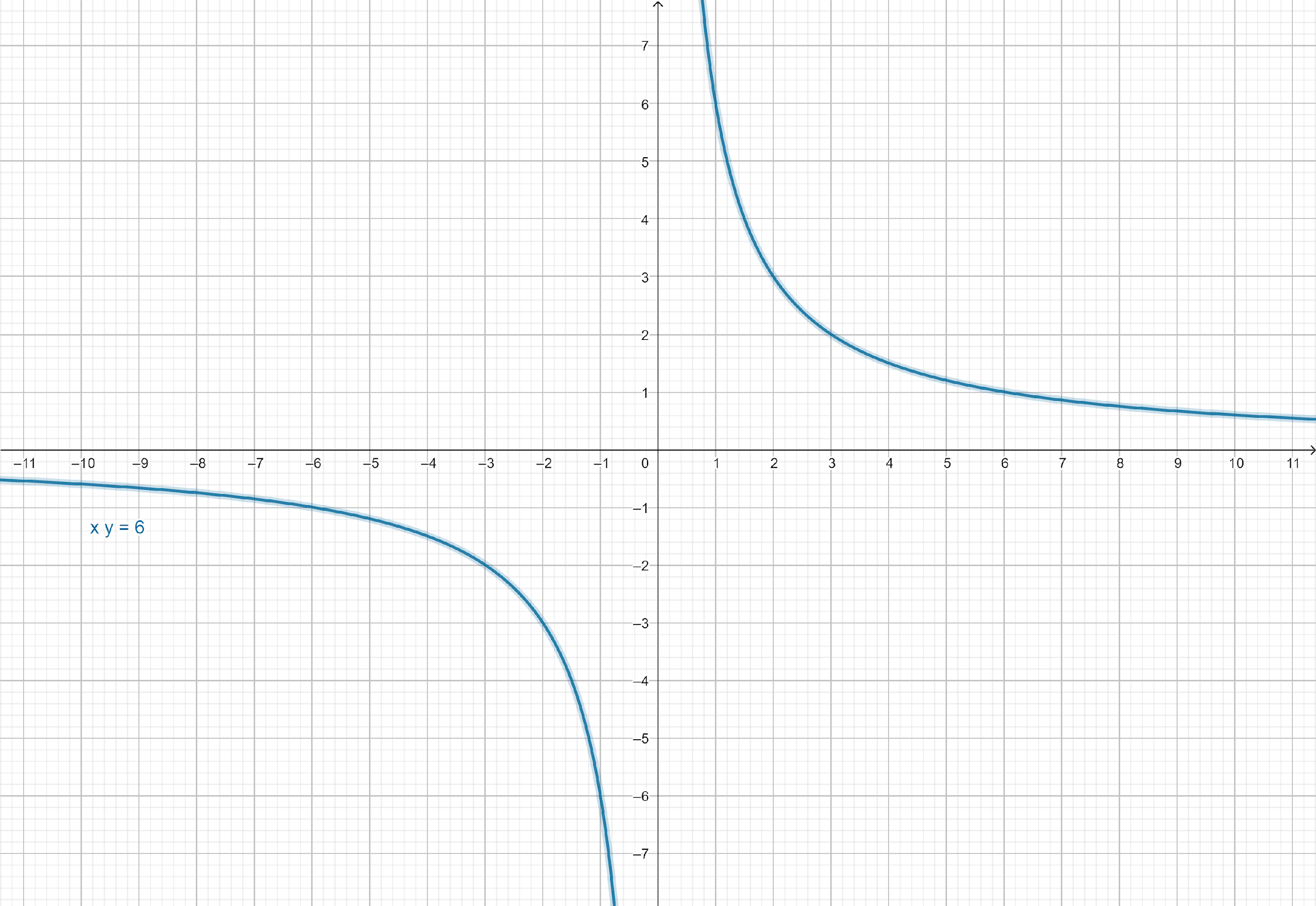
From the graph, we can observe that $xy = 6$ is a hyperbola.