
Determine the graph of the equation \[y = 2x - 3\] ?
Answer
497.7k+ views
Hint: To determine the graph we need different \[x\] values as well as their corresponding values of \[y\]. To solve this question, we take any value of \[x\] and then find the corresponding value of \[y\] and vice versa. In this way, we find two points and plot them on the graph and join them in order to get the graph of the equation.
Complete answer:
Given equation is \[y = 2x - 3\]
To plot a graph of the given equation \[y = 2x - 3\], we need points.
To find the first point let us put \[x = 0\] and find the corresponding value of \[y\].
On putting the value \[x = 0\] in the given equation.
\[y = 2 \times 0 - 3\]
On simplifying we get the value of \[y\]
\[ \Rightarrow y = - 3\]
This means when $x=0$, the value of $y$ on the graph is $-3$. On observing the values of \[x\] and \[y\] we get the first point.
\[A\] be the first point. \[A = \left( {0, - 3} \right)\]
To find the second point we put \[y = 0\] and find the corresponding value of \[x\].
On putting the value \[y = 0\] in the given equation.
\[0 = 2 \times x - 3\]
On taking 3 to another side
\[2 \times x = 3\]
On simplifying we get the value of \[x\]
\[ \Rightarrow x = \dfrac{3}{2}\]
\[ \Rightarrow x = 1.5\]
On observing the values of \[x\] and \[y\] we get the second point.
\[B\] be the first point. \[B = \left( {1.5,0} \right)\]
Now we make a table of these points.
Now we put these points in the graph and join them to obtain the graph of the equation.
On putting these points in the graph. The graph looks like-
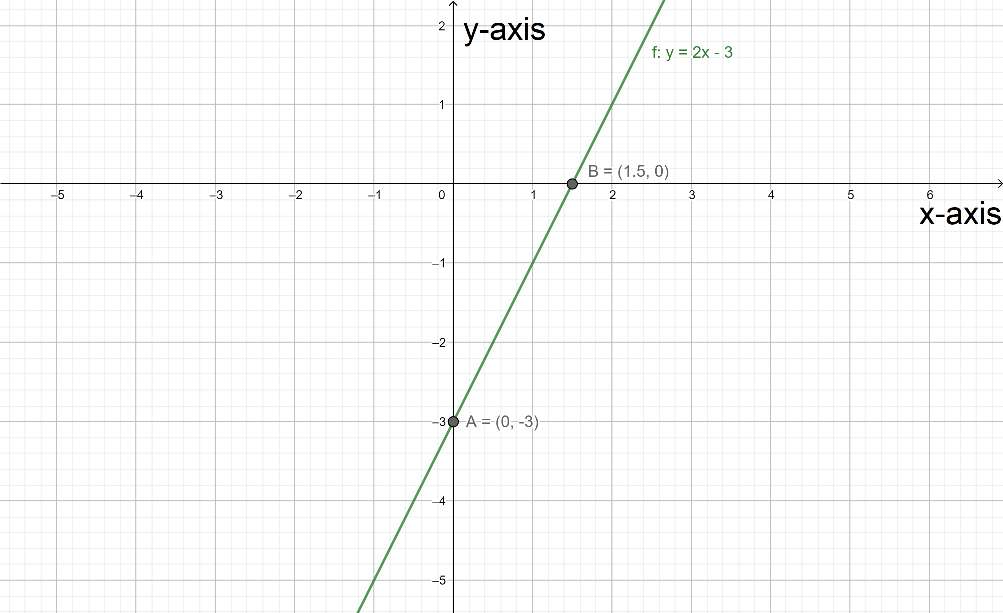
Note:
To plot the graph of the linear equation we need a minimum of two points but we are unable to make a line with a single point. More points are required if we make a curve then more points are required and with more points, our curve is more accurate.
Complete answer:
Given equation is \[y = 2x - 3\]
To plot a graph of the given equation \[y = 2x - 3\], we need points.
To find the first point let us put \[x = 0\] and find the corresponding value of \[y\].
On putting the value \[x = 0\] in the given equation.
\[y = 2 \times 0 - 3\]
On simplifying we get the value of \[y\]
\[ \Rightarrow y = - 3\]
This means when $x=0$, the value of $y$ on the graph is $-3$. On observing the values of \[x\] and \[y\] we get the first point.
\[A\] be the first point. \[A = \left( {0, - 3} \right)\]
To find the second point we put \[y = 0\] and find the corresponding value of \[x\].
On putting the value \[y = 0\] in the given equation.
\[0 = 2 \times x - 3\]
On taking 3 to another side
\[2 \times x = 3\]
On simplifying we get the value of \[x\]
\[ \Rightarrow x = \dfrac{3}{2}\]
\[ \Rightarrow x = 1.5\]
On observing the values of \[x\] and \[y\] we get the second point.
\[B\] be the first point. \[B = \left( {1.5,0} \right)\]
Now we make a table of these points.
| \[x\] | \[y\] |
| 0 | -3 |
| 1.5 | 0 |
Now we put these points in the graph and join them to obtain the graph of the equation.
On putting these points in the graph. The graph looks like-

Note:
To plot the graph of the linear equation we need a minimum of two points but we are unable to make a line with a single point. More points are required if we make a curve then more points are required and with more points, our curve is more accurate.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




