Question

Determine the area under the curve $y=\sqrt{{{a}^{2}}-{{x}^{2}}}$, included between the lines x= 0 and x= 4

Answer 1

Hint: Find the area in two different cases. When a is less than 4 and when a is greater or equal to 4. Observe that when a is less than 4, the whole curve in the domain x=0 to x= a will be included and the abscissae after x=a will be out from the domain. When a is greater or equal to 4, the whole curve in the domain x=0 to x= 4 will be included. Use the fact that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$. Hence find the required area in the two different cases.

Complete step-by-step answer:
The above question can be solved in two cases:
Case I $a\le 4$:

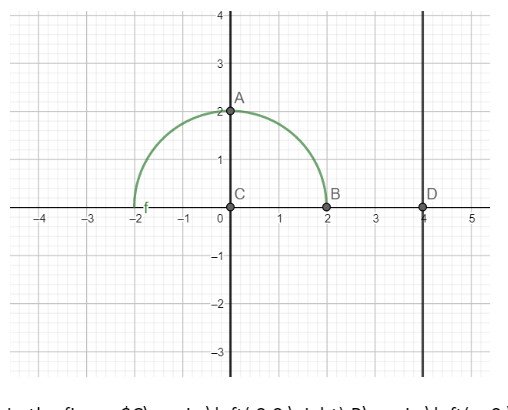
In the figure $C\equiv \left( 0,0 \right),B\equiv \left( a,0 \right)$ and $D\equiv \left( 4,0 \right)$
When $a\le 4$, we have $x\in \left( a,4 \right]$ i.e. from B to D will be outside the domain. Hence when finding the area bounded by the curve $y=\sqrt{{{a}^{2}}-{{x}^{2}}}$ , the x-axis and the ordinates x= 0 and x= 4, we will include the whole curve between x= 0 and x= a., i.e. the area of the region ABCA.
Hence the area will be the area bounded by $y=\sqrt{{{a}^{2}}-{{x}^{2}}}$, the x-axis and the ordinates x= 0 and x =a
We know that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$.
Hence, we have $A=\int_{0}^{a}{\left| \sqrt{{{a}^{2}}-{{x}^{2}}} \right|dx}$
Since $\sqrt{x}\ge 0$, we have
$A=\int_{0}^{a}{\sqrt{{{a}^{2}}-{{x}^{2}}}dx}$
Put $x=a\sin t$
Differentiating both sides with respect to t, we get
$dx=a\cos tdt$
When x= 0, we have $a\sin t=0\Rightarrow t=0$
When x= a, we have $a\sin t=a\Rightarrow a=\dfrac{\pi }{2}$
Hence, we have $A=\int_{0}^{a}{\sqrt{{{a}^{2}}-{{a}^{2}}{{\sin }^{2}}t}a\cos tdt}=\int_{0}^{\dfrac{\pi }{2}}{{{a}^{2}}{{\cos }^{2}}tdt}$
Now, we know that $\int{{{\cos }^{2}}tdt=\int{\dfrac{1+\cos 2t}{2}dt=\dfrac{t}{2}+\dfrac{\sin 2t}{4}+C}}$
Hence, we have
$A={{a}^{2}}\left( \left. \dfrac{t}{2}+\dfrac{\sin 2t}{4} \right|_{0}^{\dfrac{\pi }{2}} \right)=\dfrac{\pi {{a}^{2}}}{4}$
Case II: When $a\ge 4$

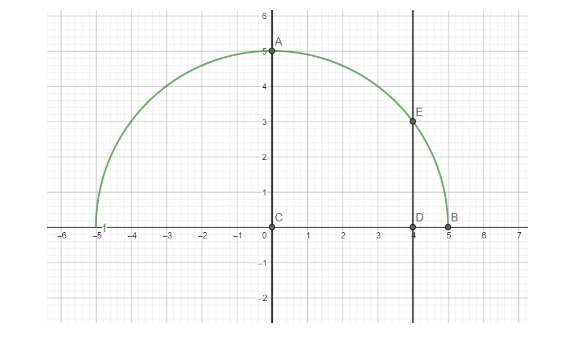
In this case, the required area is AEDCA, which is the area bounded by the curve $y=\sqrt{{{a}^{2}}-{{x}^{2}}}$, the x-axis and the ordinates x=0 and x=4
We know that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x=b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$.
Hence, we have
$A=\int_{0}^{4}{\sqrt{{{a}^{2}}-{{x}^{2}}}}$
Put $x=a\sin t$
Differentiating both sides with respect to t, we get
$dx=a\cos tdt$
When x= 0, we have $a\sin t=0\Rightarrow t=0$
When x= 4, we have $a\sin t=4\Rightarrow a={{\sin }^{-1}}\dfrac{4}{a}$
Hence, we have
$A={{a}^{2}}\int_{0}^{{{\sin }^{-1}}\dfrac{4}{a}}{{{\cos }^{2}}t}$
Now, we know that $\int{{{\cos }^{2}}tdt=\int{\dfrac{1+\cos 2t}{2}dt=\dfrac{t}{2}+\dfrac{\sin 2t}{4}+C}}$
Hence, we have
$A={{a}^{2}}\left( \left. \dfrac{t}{2}+\dfrac{\sin 2t}{4} \right|_{0}^{{{\sin }^{-1}}\dfrac{4}{a}} \right)={{a}^{2}}\left( \dfrac{{{\sin }^{-1}}\dfrac{4}{a}}{2}+\dfrac{\sin \left( 2{{\sin }^{-1}}\dfrac{4}{a} \right)}{4} \right)$
We know that $\sin \left( 2x \right)=2\sin x\cos x$
Hence, we have
$\sin \left( 2{{\sin }^{-1}}\dfrac{x}{a} \right)=2\sin \left( {{\sin }^{-1}}\dfrac{4}{a} \right)\cos \left( {{\sin }^{-1}}\dfrac{4}{a} \right)$
We know that $\cos \left( {{\sin }^{-1}}\dfrac{4}{a} \right)=\sqrt{1-{{\left( \dfrac{4}{a} \right)}^{2}}}$
Hence, we have $\sin \left( 2{{\sin }^{-1}}\dfrac{4}{a} \right)=\dfrac{8}{a}\sqrt{1-{{\left( \dfrac{4}{a} \right)}^{2}}}$
Hence, we have
$A={{a}^{2}}\left( \dfrac{{{\sin }^{-1}}\dfrac{4}{a}}{2}+\dfrac{\dfrac{8}{a}\sqrt{1-{{\left( \dfrac{2}{a} \right)}^{2}}}}{4} \right)={{a}^{2}}\left( \dfrac{{{\sin }^{-1}}\dfrac{4}{a}}{2}+\dfrac{2\sqrt{1-{{\left( \dfrac{4}{a} \right)}^{2}}}}{a} \right)=\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{4}{a}+2\sqrt{{{a}^{2}}-16}$
Note: Alternatively in case I, the value of A can be found by observing that it is the area of a quarter of a circle of radius and hence is equal to $\dfrac{\pi {{a}^{2}}}{4}$ and in the case II, the value of A can be found by using the property that $\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}}$
Hence, we have
$A=\left. \dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a} \right|_{0}^{4}=2\sqrt{{{a}^{2}}-16}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{4}{a}$, which is the same as obtained above.