
Determine graphically the coordinates of the vertices of a triangle, the equations of whose sides are given by $2y - x = 8$,$5y - x = 14$and $y - 2x = 1$.
Answer
550.2k+ views
Hint: Here, we are required to find the vertices of the triangle graphically whose equations of the sides are given. We will find the points which are satisfying each equation respectively. Plotting these points on a graph and joining them together, will give us the required lines showing these equations; which will be intersecting to form the required triangle. We will mark the coordinates of the triangle formed, hence, determining the required vertices of the triangle.
Complete step-by-step answer:
According to the question,
The given equations of the sides of a triangle are: $2y - x = 8$, $5y - x = 14$ and $y - 2x = 1$.
Now, for the equation; $2y - x = 8$
This can also be written as:
$x = 2y - 8$
Hence, for $y = 4$
$x = 2\left( 4 \right) - 8 = 0$
And for $y = 2$
$x = 2\left( 2 \right) - 8 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
Now, for the equation $5y - x = 14$
This can also be written as:
$x = 5y - 14$
Hence, for $y = 3$
$x = 5\left( 3 \right) - 14 = 1$
And for $y = 2$
$x = 5\left( 2 \right) - 14 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
Also, for the equation $y - 2x = 1$
This can also be written as:
$y = 2x + 1$
Hence, for $x = 0$
$y = 2\left( 0 \right) + 1 = 1$
And for $x = - 1$
$y = 2\left( { - 1} \right) + 1 = - 2 + 1 = - 1$
Therefore, we can draw the table, showing the points satisfying this equation:
Now, we will draw a graph showing all the given equations by plotting the above points from their respective tables and joining them to form a triangle.
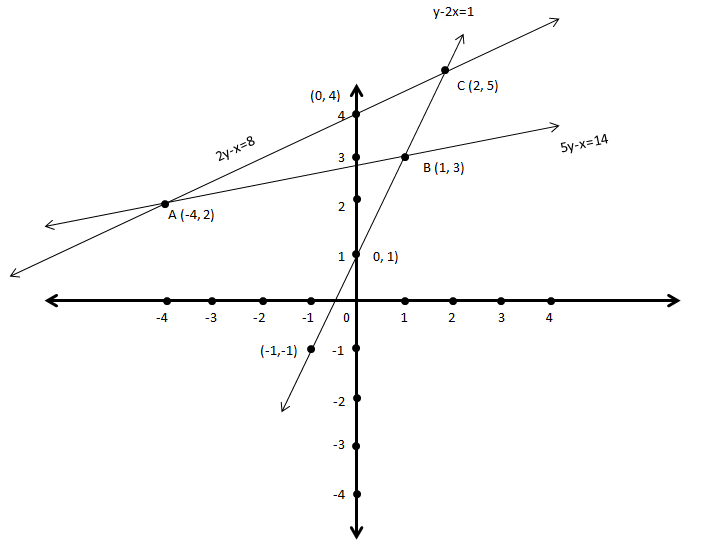
From the above graph; which is showing the lines representing the given equations, we can see that these lines are intersecting with each other to form a triangle.
We have marked the intersecting points forming the triangle $ABC$ as $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$ respectively. Hence, the required coordinates of the vertices of the triangle formed by the given equations are $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$.
Therefore, this is the required answer.
Note: In this question, we have found the points satisfying each equation and then we plotted them on a graph to find the vertices of the required triangle. An alternate way of finding the vertices when the equations of the sides are given is that, we can eliminate the three equations by taking two of them at a time and hence, finding the coordinates of the vertices simultaneously. When the vertices are found, we can plot them directly on a graph and join them together to get the required triangle. But since, in this question we were required to determine graphically the vertices of a triangle, hence, we followed the above method. If it was not asked specifically to determine the vertices graphically, then we could have used this alternate method.
Complete step-by-step answer:
According to the question,
The given equations of the sides of a triangle are: $2y - x = 8$, $5y - x = 14$ and $y - 2x = 1$.
Now, for the equation; $2y - x = 8$
This can also be written as:
$x = 2y - 8$
Hence, for $y = 4$
$x = 2\left( 4 \right) - 8 = 0$
And for $y = 2$
$x = 2\left( 2 \right) - 8 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
| x | -4 | 0 |
| y | 2 | 4 |
Now, for the equation $5y - x = 14$
This can also be written as:
$x = 5y - 14$
Hence, for $y = 3$
$x = 5\left( 3 \right) - 14 = 1$
And for $y = 2$
$x = 5\left( 2 \right) - 14 = - 4$
Therefore, we can draw the table, showing the points satisfying this equation:
| x | -4 | 1 |
| y | 2 | 3 |
Also, for the equation $y - 2x = 1$
This can also be written as:
$y = 2x + 1$
Hence, for $x = 0$
$y = 2\left( 0 \right) + 1 = 1$
And for $x = - 1$
$y = 2\left( { - 1} \right) + 1 = - 2 + 1 = - 1$
Therefore, we can draw the table, showing the points satisfying this equation:
| x | -1 | 0 |
| y | -1 | 1 |
Now, we will draw a graph showing all the given equations by plotting the above points from their respective tables and joining them to form a triangle.

From the above graph; which is showing the lines representing the given equations, we can see that these lines are intersecting with each other to form a triangle.
We have marked the intersecting points forming the triangle $ABC$ as $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$ respectively. Hence, the required coordinates of the vertices of the triangle formed by the given equations are $A\left( { - 4,2} \right)$, $B\left( {1,3} \right)$ and $C\left( {2,5} \right)$.
Therefore, this is the required answer.
Note: In this question, we have found the points satisfying each equation and then we plotted them on a graph to find the vertices of the required triangle. An alternate way of finding the vertices when the equations of the sides are given is that, we can eliminate the three equations by taking two of them at a time and hence, finding the coordinates of the vertices simultaneously. When the vertices are found, we can plot them directly on a graph and join them together to get the required triangle. But since, in this question we were required to determine graphically the vertices of a triangle, hence, we followed the above method. If it was not asked specifically to determine the vertices graphically, then we could have used this alternate method.
Recently Updated Pages
Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 Maths: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Maths: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




