Question

Describe the working of a Carnot engine and mention the expression for its efficiency.

Answer 1

Hint: A Carnot cycle is a reversible, thermodynamic system which gives the greatest efficiency for all heat engines. It has four main processes and the system undergoes successive expansions and compressions. During expansion gas does work on the surroundings and in compression, work is done on the gas by the surroundings.

Complete step-by-step solution:
Carnot cycle is a thermodynamic process in which heat is converted to work and vice versa. Ideally, it has the maximum efficiency for a heat engine. It has three main components; The source (kept at temperature, ${{T}_{1}}$), the sink (kept at temperature ${{T}_{2}}$), and the working substance.

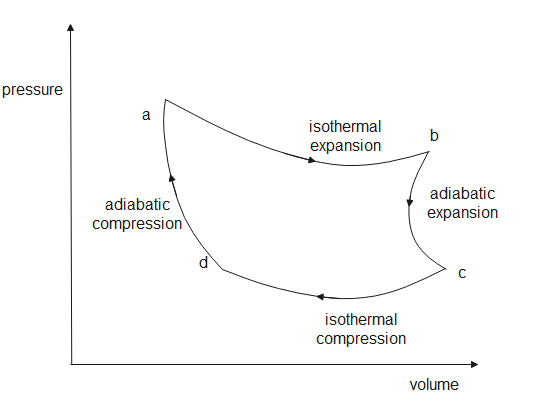
In a Carnot cycle, there are four successive operations; isothermal expansion, adiabatic expansion, isothermal compression and adiabatic compression.
At point (a), the working substance is an ideal gas; it absorbs heat from the source which is at ${{T}_{1}}$ temperature. The heat absorbed is ${{q}_{1}}$. Since temperature is constant, the gas expands and work is done by the gas on the surroundings.
At point (b), the gas undergoes adiabatic expansion, which means that no heat exchange takes place, so the gas continues to expand and work is done on the surroundings. Since no heat changes can take place, the temperature of the gas decreases to ${{T}_{1}}'$.
At point (c), the work is done on the gas by the surroundings, as temperature is constant heat loss takes place. The heat lost is ${{q}_{2}}$ at temperature ${{T}_{1}}'$.
At point (d), the process is adiabatic compression, surroundings do work on the gas and since the heat is constant, the temperature rises to ${{T}_{1}}$.
Therefore, the Carnot cycle is reversible in nature. It works on the Carnot theorem which states that for any system working between two temperatures, ${{T}_{1}}$ (sink) and ${{T}_{2}}$ (source), it can never have efficiency more than a Carnot cycle working between the same reservoirs.
In a Carnot cycle, the efficiency is given by-
$e=1-\dfrac{{{T}_{2}}}{{{T}_{1}}}$
Here, $e$ is the efficiency of the Carnot cycle.

Therefore, the Carnot cycle is a reversible, thermodynamic cycle which has four main processes and its efficiency is $e=1-\dfrac{{{T}_{2}}}{{{T}_{1}}}$.

Note:
In isothermal processes temperature remains constant while in adiabatic processes heat remains constant. By convention, the work done by the gas on the surroundings is negative while the work done on the gas by the surroundings is positive. The efficiency is a unitless quantity.