Question

Describe how the two figures at the right are alike and how they are different. Which box has larger lateral surface area?

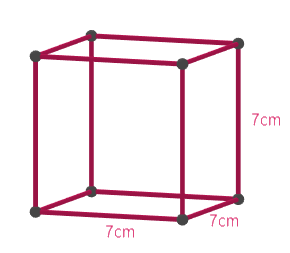
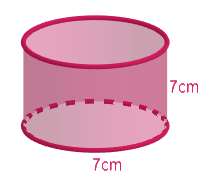
Answer 1

Hint: Try to recall the different examples of things which are cubic and cylindrical in shape and we use in our day today life, for example: pencil box, laptops, boxes etc. Also, remember that the cube has six faces and 12 edges while the cylinder has 2 faces only. The lateral surface area of the cylinder is given by $2\pi rh$ and of the cube is given by $4{{a}^{2}}$.

Complete step by step solution:
In mathematics, the word cube refers to a polyhedron which consists of squares as its faces. However the faces of a cylinder is not a polygon, so it is not a polyhedron.
Now if we talk about their similarities, both of them have the same height and we know that both cylinder and cube the volume is given by base area multiplied by height. Also, both are 3 dimensional symmetric structures.
Now let us draw a diagram for better visualisation.
 

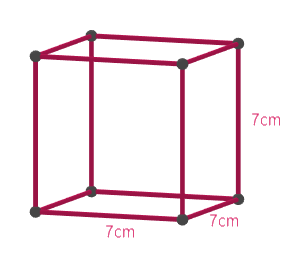
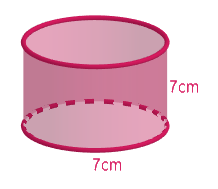
Now let us move to find the lateral surface area of the cube and the cylinder boxes. Let us first find the lateral surface area of the cube. We know that the lateral surface area of the cube is given by $4{{a}^{2}}$ , where a is its side length which will be equal to 7cm in our case.
$\text{Lateral surface area of the cube}=4{{a}^{2}}=4\times {{7}^{2}}=196c{{m}^{2}}$
Now we will find the lateral surface area of the cylinder. The lateral surface area of the cylinder is given by $2\pi rh$ , in our case a is equal to half of 7cm and height is 7cm.
$\text{Lateral surface area of the cylinder}=2\pi rh=2\times \dfrac{22}{7}\times \dfrac{7}{2}\times 7=154c{{m}^{2}}$

Note: It is important that you remember the formulas related to their total and lateral surface areas because that is the key to these questions. Also, remember the value of $\pi $ both in decimal and fraction form, i.e., $\pi =\dfrac{22}{7}\text{ or 3}\text{.14}$ and use them according to the need in the formulas.