Question

Derive the following expression for the refraction at concave spherical surface:
 $ \dfrac{\mu }{v} - \dfrac{1}{u} = \dfrac{{\mu - 1}}{R}. $

Answer 1

Hint
A spherical mirror is a part of a sphere with a reflecting surface. If the inner surface is the reflective surface then the mirror is called a concave mirror and if the outer surface is the reflecting surface then the mirror is called a convex mirror. Here we have a concave reflecting surface for which we have to derive the given expression.

Complete step by step answer
Let us consider a concave mirror as shown in the diagram below,

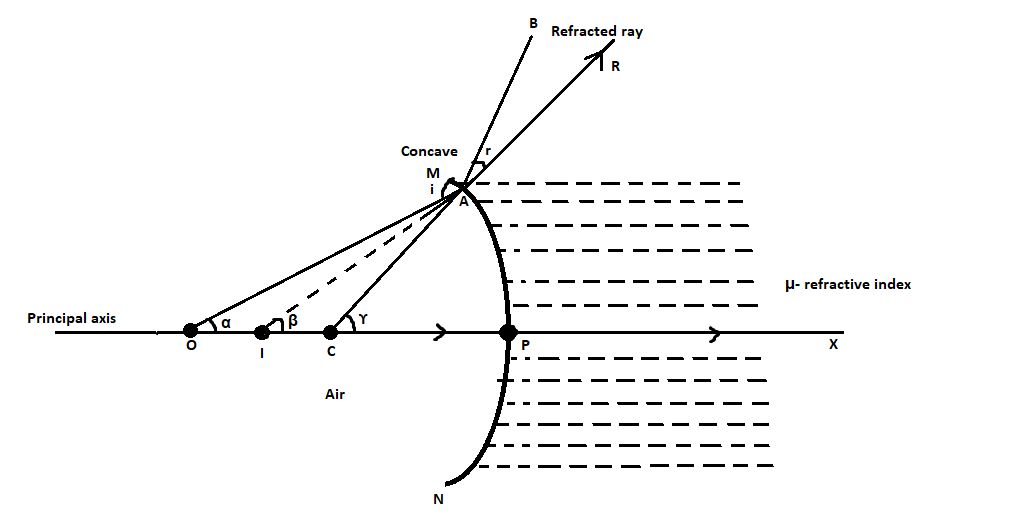
The concave mirror is represented by $ MPN $ . The refractive index of the medium of the spherical surface is given by $ \mu $ . We consider $ P $ as the pole of the mirror, $ O $ as the centre of curvature, and $ PC $ represents the principal axis of the refractive spherical surface. We consider a point object at $ O $ . An incident ray travels through $ C $ and it is normal to the spherical surface. It will not undergo any refraction hence it will travel in a straight line along $ PX $ . Another ray that we consider is $ OA $ . It will refract at the point $ A $ bending towards the normal. At a point $ i $ we will get a virtual image.
Let us consider the ray angles with the principal axis to be $ \alpha,\beta $ , and $ \gamma $ respectively.
According to Snell’s law, we can write the refractive index as
 $\Rightarrow \mu = \dfrac{{\sin i}}{{\sin r}} $
Where $ i $ is the angle of incidence and $ r $ is the angle of refraction.
Here we have very small $ i $ and $ r $ , hence we can write,
 $\Rightarrow \sin i = i $ And $ \sin r = r $ in equation
We get,
 $\Rightarrow \mu = \dfrac{i}{r} $
From this we get,
 $\Rightarrow i = \mu r $
By using the exterior angle theorem, from $ \Delta AOC $ we get,
 $\Rightarrow \gamma = i + \alpha $
From this we get
 $\Rightarrow i = \gamma - \alpha $
Now, by using exterior angle theorem in $ \Delta IAC $ , we get
 $\Rightarrow \gamma = \beta + r $
From this we get,
 $\Rightarrow r = \gamma - \beta $
Substituting these values of $ i $ and $ r $ in equation we get,
 $\Rightarrow \left( {\gamma - \alpha } \right) = \mu \left( {\gamma - \beta } \right) $
For a spherical surface, we can write the angle as
 $\Rightarrow angle = \dfrac{{arc}}{{radius}} $
We can write
 $\Rightarrow \alpha = \dfrac{{PA}}{{OP}} $
And
 $\Rightarrow \beta = \dfrac{{PA}}{{IP}} $
Also
 $\Rightarrow \gamma = \dfrac{{PA}}{{CP}} $
Substituting these values of $ \alpha ,\beta $ and $ \gamma $ in , we get
 $\Rightarrow \dfrac{{PA}}{{PC}} - \dfrac{{PA}}{{PO}} = \mu \left( {\dfrac{{PA}}{{PC}} - \dfrac{{PA}}{{PI}}} \right) $
Taking the common terms outside we get,
$\Rightarrow PA\left( {\dfrac{1}{{PC}} - \dfrac{1}{{PO}}} \right) = \mu PA\left( {\dfrac{1}{{PC}} - \dfrac{1}{{PO}}} \right)$
 $\Rightarrow PA $ gets cancelled as it is common on both sides. Now we have
 $\Rightarrow \dfrac{1}{{PC}} - \dfrac{1}{{PO}} = \mu \left( {\dfrac{1}{{PC}} - \dfrac{1}{{PI}}} \right) $
Now we have to apply the sign convention.
 $\Rightarrow PC = - R $ (where $ R $ is the radius of curvature)
 $\Rightarrow PI = - v $ (Where $ v $ is the distance of the image from the pole of the mirror)
 $\Rightarrow PO = - u $ (Where $ u $ is the distance of the object from the pole of the mirror)
Putting these values in equation
We get,
 $\Rightarrow \left( {\dfrac{1}{{ - R}}} \right) - \left( {\dfrac{1}{{ - u}}} \right) = \mu \left( {\dfrac{1}{{ - R}} + \dfrac{1}{v}} \right) $
Opening the brackets on LHS
$\Rightarrow\dfrac{{ - 1}}{R} + \dfrac{1}{u} = \mu \left( {\dfrac{{ - 1}}{R} + \dfrac{1}{v}} \right)$
Opening the brackets on RHS
 $\Rightarrow \dfrac{{ - 1}}{R} + \dfrac{1}{u} = \dfrac{\mu }{R} + \dfrac{\mu }{v} $
Rearranging, we get
 $\Rightarrow \dfrac{{ - 1}}{R} + \dfrac{\mu }{R} = \dfrac{\mu }{v} - \dfrac{1}{u} $
We can write this expression as,
 $\Rightarrow \dfrac{{\mu - 1}}{R} = \dfrac{\mu }{v} - \dfrac{1}{u} $
Hence we got the required expression for the concave refractive surface.

Note
According to the Cartesian sign convention,
-All distances as measured from the pole of the mirror.
-The distances that are measured in the direction of the incident light are taken as positive.
-The distances that are measured opposite to the direction of incident light is considered as negative.
-The height measured upward the principal axis is measured as positive and the height measured downward is measured negative.