Question

Derive the condition for balance of a Wheatstone's bridge using Kirchhoff's rules.

Answer 1

Hint: Draw the Wheatstone bridge circuit diagram first and then try to analyse the condition. By using the notion of current flow and voltage division, try to understand the concept of the bridge and obtain the required balanced condition. The circuit laws of Kirchhoff are two equalities dealing with the current and potential difference in the electrical circuit lumped element model.

Complete answer:
It can be mathematically expressed, as per Kirchhoff's first rule, as:
$\Sigma i=0$
Where $\Sigma i$ is the sum of current entering the junction and current leaving the junction.
It can be mathematically expressed, as per Kirchhoff's first rule, as:
$\Sigma i R=\Sigma E$
Where $\Sigma R$ is the resistance at the junction and $\Sigma E$ is the emf at the junction.

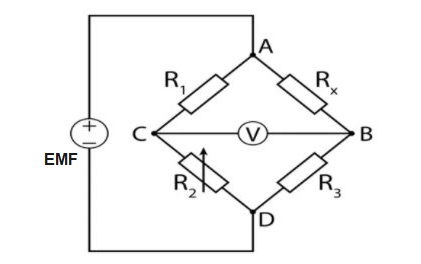
Here $G$ is the galvanometer and it is used to measure the current flowing across two points.
And $R_{1}, R_{2}, R_{3}$ and $R_{x}$ are the resistances connected as shown in the above diagram.
Across the points and as shown, the resistances are related. If the current flows through the circuit and the circuit,
No deflection is provided by the galvanometer, so the bridge is balanced. We must have the conditions for a balanced bridge.
as:
$\dfrac{R_{x}}{R_{3}}=\dfrac{R_{1}}{R_{2}}$
Let the total current flowing in the circuit be I. Now this current is divided into two parts $i_1$ and $i_2$ flowing through
$R_{x}, R_{3}$ and $R_{1}, R_{2} .$ When the Wheatstone is balanced, the galvanometer shows zero deflection, that is the potential
of $B$ and $C$ will be equal. In the closed circuit ABCD, by Kirchhoff's second law, we will have:
$\Rightarrow i_{1} R_{1}-i_{2} R_{x}=0$
$\Rightarrow i_{1} R_{1}=i_{2} R_{x}$ - -equation 1
And
$i_{1} R_{2}-i_{2} R_{3}=0$
$\Rightarrow i_{1} R_{2}=i_{2} R_{3}$ - -equation 2
Dividing equation 1 by equation 2, we have $\dfrac{i_{1} R_{1}}{i_{1} R_{2}}=\dfrac{i_{2} R_{x}}{i_{2} R_{3}}$
$\therefore \dfrac{R_{1}}{R_{2}}=\dfrac{R_{x}}{R_{3}}$
Which is the required condition.

Note:
Remember that Kirchhoff's law has two rules. Using both the rules, the condition for balanced Wheatstone may be obtained. The laws of Kirchhoff are used to study any type of circuit, whether the circuit is simple or complex.