Question

Derive mirror equation. State any three experimental observations of photoelectric emission.

Answer 1

Hint: In a spherical mirror, the distance of the object from its pole is called the object distance (u). The distance of the image from the pole of the mirror is called the image distance (v). The distance of the principal focus from the pole is called the focal length (f). There is a relationship between these three quantities given by the mirror formula which is expressed as $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$.This formula is valid in all situations for all spherical mirrors for all positions of the object.

Complete step by step solution:
Derivation of the Mirror Formula

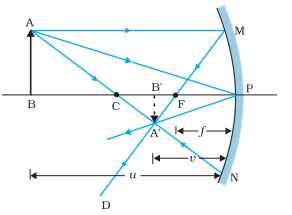
We now derive the mirror equation or the relation between the object distance (u), image distance (v) and the focal length (f). In the above figure, the two right-angled triangles A′B′F and MPF are similar.
$
   \Rightarrow \dfrac{{{B'}{A'}}}{{PM}} = \dfrac{{{B'}F}}{{FP}} \\
   \Rightarrow \dfrac{{{B'}{A'}}}{{BA}} = \dfrac{{{B'}F}}{{FP}} \\
  \because PM = AB...............(1) \\
   \Rightarrow \angle APB = \angle {A'}PB \\
  \therefore \Delta {A'}{B'}{P'} \sim \Delta A{B'}P \\
  \therefore \dfrac{{{B'}{A'}}}{{BA}} = \dfrac{{{B'}P}}{{BP}}............(2) \\
  By{\text{ }}comparing{\text{ }}equation(1){\text{ }}and{\text{ }}(2),{\text{ }}we{\text{ }}get \\
   \Rightarrow \dfrac{{{B'}F}}{{FP}} = \dfrac{{{B'}P - FP}}{{FP}} = \dfrac{{{B'}P}}{{BP}} \\
   \Rightarrow {B'}P = - v,FP = - f,BP = - u \\
  U\sin g{\text{ }}these{\text{ }}in{\text{ }}equation,{\text{ }}we{\text{ }}get \\
   \Rightarrow \dfrac{{ - v + f}}{{ - f}} = \dfrac{{ - v}}{{ - u}} \\
   \Rightarrow \dfrac{{v - f}}{f} = \dfrac{v}{u} \\
  On{\text{ }}further{\text{ }}solving,{\text{ }}we{\text{ }}get \\
  \therefore \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \\
 $
Note: In a spherical mirror, the distance of the object from its pole is called the object distance (u). The distance of the image from the pole of the mirror is called the image distance (v). The distance of the principal focus from the pole is called the focal length (f). There is a relationship between these three quantities given by the mirror formula which is expressed as $\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$.This formula is valid in all situations for all spherical mirrors for all positions of the object.