Question

Define the terms vertically opposite angles, linear pair of angles, and adjacent angles with suitable diagrams.

Answer 1

Hint: Try to interpret the definitions of the terms mentioned in the question and represent them in the form of a diagram.

Complete step-by-step answer:

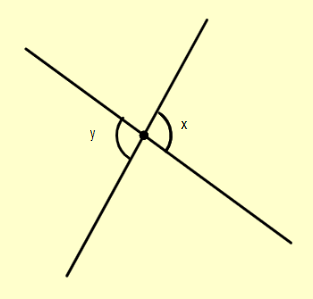
To start with the solution, we first try to describe the term vertically opposite angles. When two lines intersect at a point, then the pair of angles formed, which are opposite to each other, are called vertically opposite angles. They share the same vertex and are equal to mathematically. Vertically opposite angles can be represented by the diagram as:

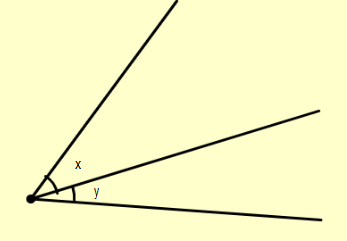
Now let’s move to adjacent angles. When two angles have a common side and a common corner but don’t overlap and are not the opposite, they are called adjacent angles. The diagram of adjacent angles is:

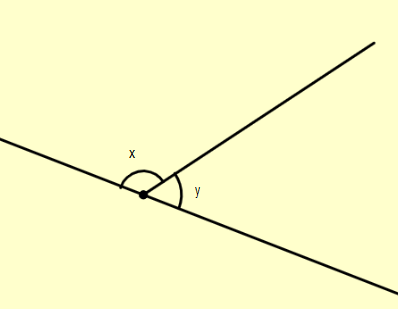
Now a linear pair of angles is defined as the pair of angles two angles that have a common side and a common corner but don’t overlap are not opposed to each other and whose sum is equal to $180{}^\circ $. We can show it in a diagram as:

Note: It is very important to learn all the properties of vertically opposite angles and adjacent angles as they are often used. Also, a point of similarity of all the pair of angles talked about in the above question is that they share the same vertex and the same intersecting lines.