Question

Define radian measure of an angle.

Answer 1

Hint: We have two methods of measuring an angle in degrees and radian. Radian is another way of expressing the measure of an angle. One radian is equal to \[57.2958\] degrees.

Complete step-by-step answer:
Radian measure of a central angle of a circle is defined as the ratio of length of the arc subtended by that angle to the length of radius of the circle. A radian is represented by the symbol rad.
To understand radian measure of an angle let us draw a circle of radius \[r\] and central angle \[\theta \] which subtends an arc of length \[l\].

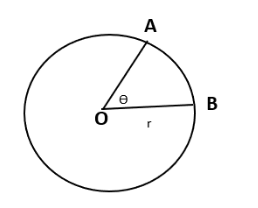
In this circle the central angle is \[\theta =\angle AOB\], \[r\] is the radius of the circle and \[AB\] is the arc subtended by the central angle.
According to the definition of radian measure of an angle is written as ratio of length of arc \[l\] subtended by central angle \[\theta \] to the radius of circle \[r\].
\[\theta =\dfrac{l}{r}\]
We can represent \[\theta \] as one radian when \[l=r\],
\[\theta =\dfrac{r}{r}=1\]
Now, let us look into the calculation of one radian in degrees.
Let us take a semicircle, we know that the central angle subtended by a semicircle is \[{{180}^{\circ }}\] . Number of radians required to represent the central angle of the semicircle is calculated as approximately \[3.1415\] radians which is equal to \[\pi \].
We must recall that \[\pi \] is the real number constant which is defined as the ratio of diameter of the circle divided by the circumference of the circle which is approximately equal to \[3.1415\].
So, we have seen that \[\pi \] radian is equal to \[{{180}^{\circ }}\]. Therefore, we can write that
\[1\] radian = \[\dfrac{{{180}^{\circ }}}{\pi }={{57.2958}^{\circ }}\]
How to convert degrees into radians and radians into degrees?
To convert degrees into radians, multiply the angle by \[\dfrac{\pi }{180}\]
To convert radians into degrees, multiply the angle by \[\dfrac{180}{\pi }\]

Note: Don’t get confused between degrees and radian measure of an angle. Whenever definition is asked, we must make sure to draw the diagram and mark the necessary details in it. This will make it easy for us to recollect the definition and use all the terms related to it. This will fetch us good grades in the exams too. Keep in mind the basic difference that radian measure relates arc length and radius of a circle whereas degree measure relates circumference and diameter of the circle.