Question

Define oscillatory motion.

Answer 1

Hint: A motion is said to be oscillatory if its diagram in displacement-time graph is either
A. Sinusoidal with constant amplitude. (undamped)
B. Sinusoidal with decreasing amplitude. (damped)

Complete step-by-step answer:
We first need to know about the simple harmonic motion where the force on a body is proportional to its displacement from a mean position. Its equation of motion can be given by,
$$m\dfrac{d^2y}{dt^2}+R\dfrac{dy}{dt}+ky=0$$
Where R is the damping force per unit velocity of the object. k is called the force constant. The equation is modified as,
$$\dfrac{d^2y}{dt^2}+2b\dfrac{dy}{dt}+\omega_0^2y=0$$
Here, $$2b=\dfrac{R}{m}$$ and $$\omega_0^2=\dfrac{k}{m}$$
Undamped oscillatory motion- In this case, R=0 $$\Rightarrow$$ b=0. Hence the equation reduces to,
$$\dfrac{d^2y}{dt^2}+\omega_0^2y=0$$
The solution will be, $$y=A.cos(\omega_0t-\theta) $$
Where, A is the amplitude of oscillation and $$\theta$$ depends on the initial conditions. Its diagram looks like…..

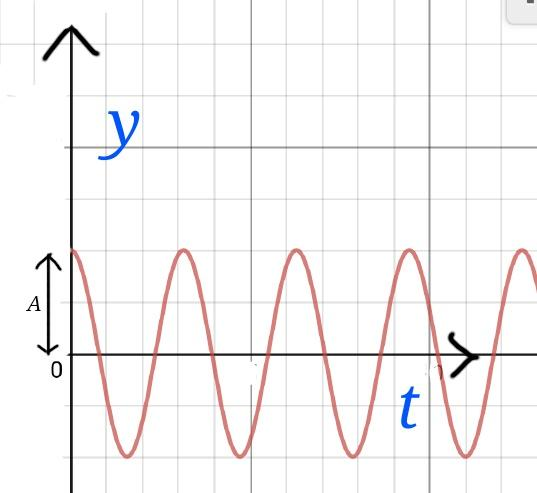
Its energy is given by,
$$E=E_k+E_p=\dfrac{1}{2}m(\dfrac{dy}{dt})^2+\dfrac{1}{2}m\omega_0^2y^2\\=\dfrac{1}{2}m\omega_0^2A^2 $$
Damped oscillation- In case $$b\neq 0$$, oscillation can only be observed if $$b\leq \omega_0$$ and in all the other cases no oscillation will be observed.
If $$b\geq \omega_0$$ ,the motion is called over damped.
If $$b=\omega_0$$, the motion is said to be critically damped.
In these two cases there is no oscillation. For oscillation (damped), $$b\leq \omega_0$$
In this case, the solution is given by, $$y=A.e^{-bt}.cos(\omega t-\theta)$$
Here, $$\omega=\sqrt{\omega_0^2-b^2}$$

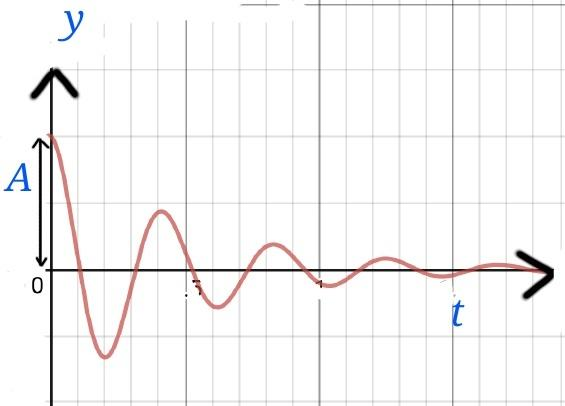
The diagram will look like this.
In this case, the amplitude decreases as , $$A_1=Ae^{-bt}$$
Its energy can be shown to be $$E=\dfrac{1}{2}m\omega_0^2A^2e^{-2bt}$$

Note: There is another type of oscillation that is called forced oscillation. In this case, the system is forced to move in oscillation by an oscillatory external force.