Question

Define many-one function. Give an example of many-one functions.

Answer 1

Hint: As we know that a function $f:X\to Y$ that is from variable $X$ to variable $Y$ is said to be one-one functions if there exist only one element from domain connected with only one and unique element from co-domain. Similarly ,we can say that a function$f:X\to Y$ that is from variable $X$ to variable $Y$ is said to be many-one functions if there exist two or more elements from the domain connected with the same element from the co-domain.
With the help of this definition, we can give an example, consider elements of $X$ be $\{1,2\}$ and elements of $Y$ be $\{x\}$ and $f:X\to Y$ such that $f=\{(1,x),(2,x)\}$ . here element one and two both connected with the same element that is $x$ . This is how a function can have many-one relationships.

Complete step-by-step answer:
Many-one function is defined as , A function$f:X\to Y$ that is from variable $X$ to variable $Y$ is said to be many-one functions if there exist two or more elements from a domain connected with the same element from the co-domain .
Let us consider an example ,
Let the domain or elements of $X$ be $\{1,2.3,4,5,6\}$ ,
Let the co-domain or elements of $Y$ be $\{x,y,z\}$ and
$f:X\to Y$
Such that $f=\{(1,x),(2,x),(3,x),(4,y),(5,z)\}$

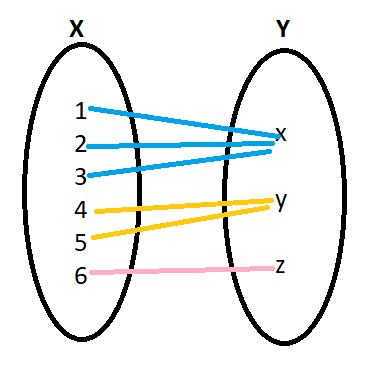
Here elements one , two and three all are connected with the same element that is $x$ , and the elements four and five are connected with the same element that is $y$. This is how a function can have many-one relationships.

Note: Range is defined as the set of elements from $y$ that actually come out whereas the co-domain of a function is given by the set of values that can possibly become a range of the function. In this particular question the range of the function is equal to the co-domain of the function.