
Define gravitational potential energy. Derive an expression for the gravitational potential in the gravitational field of the earth at a distance r from the center of the earth.
A. \[ = \dfrac{{2GMm}}{r}\]
B. \[ = \dfrac{{GMm}}{r}\]
C. \[ = \dfrac{{3GMm}}{r}\]
D. \[ = \dfrac{{4GMm}}{r}\]
Answer
613.8k+ views
Hint: In this question, we first write the equation for the force of attraction between a body and the earth that is $F = \dfrac{{mMG}}{{{y^2}}}$. Then we should write the expression for small work done $dw$ in bringing a body from a point $dy$ that is $dw = Fdy$. Then substituting the expression of F in this equation and integration from infinity to r we obtain the required potential energy as $U = - \dfrac{{GmM}}{r}$.
Complete Step-by-Step solution:
The work required in bringing an object from infinity to a point in the presence of the gravitational field is known as the gravitational potential energy.
It is represented by U that is
$U = mgh$, where m is the mass, g is the acceleration due to the gravity, h is the height
We can better understand this concept from the figure1
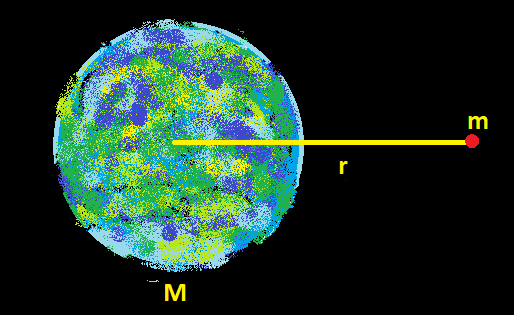
We already know that the force of attraction between a body and the Earth, when the distance of the body from the center of the Earth is y is given by:
$F = \dfrac{{mMG}}{{{y^2}}}$
Where M is the mass of the earth
m is mass of the body
G is the universal gravitational constant
Now let us assume that $dw$ is the small work done in bringing a small mass without any kind of acceleration from a point which is at a small distance $dy$ by a force F. Then we can write
$dw = Fdy$
Now we can find the total work done in bringing the mass m from infinite distance to a location that is at r distance from the center of the earth. And as work is done is same as the energy we can write
$W = U = \int_\infty ^r {\dfrac{{mMG}}{{{y^2}}}} $
$ \Rightarrow U = \int_\infty ^r {\dfrac{{mMG}}{{{y^2}}}} = \left. { - \dfrac{{mMG}}{{{y^{ - 1}}}}} \right|_\infty ^r$
$ \Rightarrow U = \left. { - \dfrac{{mMG}}{{{y^1}}}} \right|_\infty ^r = - \dfrac{{mMG}}{r} + 0$
$ \Rightarrow U = - \dfrac{{mMG}}{r}$
Therefore the required expression for the gravitational potential energy is $U = - \dfrac{{GmM}}{r}$. Hence option B is correct.
Note: For these types of questions, we need to understand the meaning of gravitational potential energy, gravitational force, acceleration due to gravity, and Universal gravitational constant. We also need to know the expression related to these. Only then we will be able to solve it. We also need to know the basics of integration and for finding a total of some quantity.
Complete Step-by-Step solution:
The work required in bringing an object from infinity to a point in the presence of the gravitational field is known as the gravitational potential energy.
It is represented by U that is
$U = mgh$, where m is the mass, g is the acceleration due to the gravity, h is the height
We can better understand this concept from the figure1

Figure 1
We already know that the force of attraction between a body and the Earth, when the distance of the body from the center of the Earth is y is given by:
$F = \dfrac{{mMG}}{{{y^2}}}$
Where M is the mass of the earth
m is mass of the body
G is the universal gravitational constant
Now let us assume that $dw$ is the small work done in bringing a small mass without any kind of acceleration from a point which is at a small distance $dy$ by a force F. Then we can write
$dw = Fdy$
Now we can find the total work done in bringing the mass m from infinite distance to a location that is at r distance from the center of the earth. And as work is done is same as the energy we can write
$W = U = \int_\infty ^r {\dfrac{{mMG}}{{{y^2}}}} $
$ \Rightarrow U = \int_\infty ^r {\dfrac{{mMG}}{{{y^2}}}} = \left. { - \dfrac{{mMG}}{{{y^{ - 1}}}}} \right|_\infty ^r$
$ \Rightarrow U = \left. { - \dfrac{{mMG}}{{{y^1}}}} \right|_\infty ^r = - \dfrac{{mMG}}{r} + 0$
$ \Rightarrow U = - \dfrac{{mMG}}{r}$
Therefore the required expression for the gravitational potential energy is $U = - \dfrac{{GmM}}{r}$. Hence option B is correct.
Note: For these types of questions, we need to understand the meaning of gravitational potential energy, gravitational force, acceleration due to gravity, and Universal gravitational constant. We also need to know the expression related to these. Only then we will be able to solve it. We also need to know the basics of integration and for finding a total of some quantity.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Who Won 36 Oscar Awards? Record Holder Revealed

Why is there a time difference of about 5 hours between class 10 social science CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE




