Question

Define coaxial circles and deduce their equation in simplest form.

Answer 1

Hint:
Read and understand the definition properly. Then to ease up the calculation part, suppose that the radical axis is the y-axis and one of the circle’s centre is on the x-axis. Take the equation of the second circle be the general equation of a circle. Then find the radical axis and compare it with the equation of y-axis.

Complete step-by-step answer:
A system of circles is coaxial if every pair of circles from the system have the same radical axis. Circles passing through two fixed points form a coaxial system. Therefore, a coaxial system of circles is defined by the radical axis and any one of the circles. The equation:

$S+\lambda P=0$ represents the family of coaxial circles where S is the equation of any circle from the family of circles, P is the equation of the radical axis, and $\lambda $ is a constant.

The radical axis of two non-concentric circles is a line defined by the two circles, perpendicular to the line connecting the centres of the circles. If the circles cross, their radical axis is the line through their two crossing points.

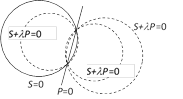
Now, we will deduce the equation of coaxial circles in the simplest form.
Let the common radical axis be chosen along the y-axis and the line of centres which will be perpendicular to the radical axis be along the x-axis.
Hence the equation of any circle will be:
${{x}^{2}}+{{y}^{2}}+2gx+c=0$ …(1)
Let any other circle of the system be:
${{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0$ …(2)
Now, we know that the radical axis of two circles: ${{S}_{1}}=0$ and ${{S}_{2}}=0$ is given by:
${{S}_{1}}-{{S}_{2}}=0$
Using this formula, we will get the equation of the radical axis of (1) and (2).
Subtracting (1) and (2), we get the following:
$2x\left( g-{{g}_{1}} \right)-2{{f}_{1}}y+\left( c-{{c}_{1}} \right)=0$ …(3)
But we assumed initially that the radical axis is y-axis i.e.: $x=0$ . …(4)
So, (3)=(4).
Comparing (3) and (4), we get:
${{f}_{1}}=0$, $c-{{c}_{1}}=0\Rightarrow c={{c}_{1}}$
Hence, any other circle of the system will have its equation of the form:
${{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+c=0$
Thus, the equation of the system of circles is:
${{x}^{2}}+{{y}^{2}}+2{{g}_{\gamma }}x+c=0$
Where, c is a constant and ${{g}_{\gamma }}$ is a parameter representing a family of coaxial circles whose common radical axis is y-axis.

Note: In the above question, we supposed that the radical axis of the family of circles is the y-axis and one of the circle’s centre is on the x-axis. This is done to ease up the calculation. If we do not do this, the calculation will get very tricky and you might end up making some mistakes.