Question

Define centripetal acceleration. Drive expression for centripetal acceleration of a particle moving with uniform speed v along a circular path of radius. Give the direction of the acceleration.

Answer 1

Hint: Centripetal acceleration occurs due to centripetal force. It is also called radial acceleration. Centripetal force tends to move a body in a circular path. It acts towards the centre of the body in which a body is traversing.


Complete step-by-step answer:
Centripetal Acceleration is the acceleration which acts towards the centre of the body. It is the property of a body. It is the property of a body performing circular motion.
It arises due to centripetal force which acts constantly towards the centre of the circle. It is perpendicular to the velocity. It is due to that change in velocity (in terms of direction such acceleration appears) 
\[ac=\dfrac{\vartriangle V}{\vartriangle t}=\dfrac{{{V}^{2}}}{R}\]
V = velocity of particle
R = Radius 
Suppose a body moving \[{{V}_{1}}\] with velocity transverses velocity changes to \[{{V}_{2}}\] .(In terms of direction) the net change in velocity generates the acceleration. 

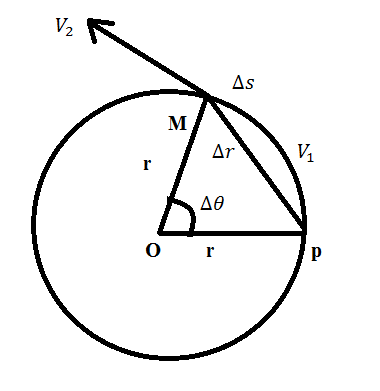
\[\vartriangle V={{V}_{2}}-{{V}_{1}}\]
\[\vartriangle s\to \]Change of radius of the length PM
\[\vartriangle r\to \]Displacement or arc length PM
As \[ac=\dfrac{\vartriangle V}{\vartriangle t}\] (the acceleration is towards center) \[\vartriangle Q\]as is small and \[\vartriangle s\approx \vartriangle r\]
.Now for magnitude,
The triangles PTR and OPM are similar above magnitude wise \[{{\text{V}}_{\text{1}}}\text{=}{{\text{V}}_{\text{2}}}\]so they form a 2 isosceles triangles.
So using property of similar triangles, 
\[\frac{\vartriangle V}{V}=\dfrac{\vartriangle s}{r}\] …… 1
Centripetal acceleration is \[\dfrac{\vartriangle V}{\vartriangle t}\]
Multiply and divide by
\[\dfrac{\vartriangle \text{V}}{\vartriangle t}=\dfrac{\vartriangle s}{\vartriangle t}\frac{V}{r}\]
\[\dfrac{\vartriangle \text{V}}{\vartriangle t}=\] Acceleration (centripetal)
And that \[\dfrac{\vartriangle s}{\vartriangle t}=\] velocity (V) = linear / tangential velocity / speed
So
\[\text{ac=}\dfrac{{{\text{V}}^{\text{2}}}}{\text{R}}\] …. 2
So we have linear or that ac is perpendicular to linear or tangential velocity 

Note: 
Centrifugal force: It is the reaction centripetal force and acts away from the centre. Its magnitude is equal to that of centripetal force.