Question

Deduce expression for the resultant potential difference, impedance and current in L-R alternating circuit. Draw a graph to show the phase difference between the current and voltage.

Answer 1

Hint: In L-R circuit an inductor and a resistance are connected in series with a voltage source. Due to current in the circuit there is potential drop across the resistor and the inductor.

Complete step by step solution:
A pure resistance $R$ and a pure inductive coil of inductance $L$ as shown connected in series along an alternating current source.

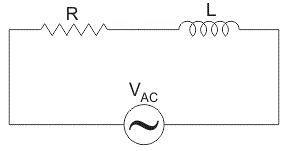
Let $V=$r.m.s. value of the applied voltage,
$I=$r.m.s value of the resultant current in the circuit.
${{V}_{R}}=IR$ is the voltage drop across the resistor which is in phase with the current $I$,
​${{V}_{L}}=I{{X}_{L}}$ is the voltage drop across the inductor which is ahead of $I$ by $90{}^\circ $.
The applied voltage from the alternating voltage source is the vector sum of the voltage drop across the resistor and the inductor.
\[\begin{align}
  & V=\sqrt{V_{R}^{2}+V_{L}^{2}} \\
 & =\sqrt{{{\left( IR \right)}^{2}}+{{\left( I{{X}_{L}} \right)}^{2}}} \\
 & =I\sqrt{{{R}^{2}}+X_{L}^{2}}
\end{align}\]​​
The quantity \[\sqrt{{{R}^{2}}+X_{L}^{2}}\]​ is known as the impedance of the circuit. Impedance of the circuit is represented as $Z$.
As seen from the impedance triangle ABC,

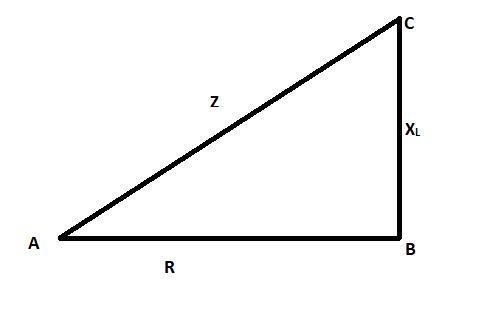
$\begin{align}
  & {{Z}^{2}}={{R}^{2}}+X_{L}^{2} \\
 & {{\left( \text{Impedance} \right)}^{2}}={{\left( \text{Resistance} \right)}^{2}}+{{\left( \text{Inductive Reactance} \right)}^{2}} \\
\end{align}$
From the given figure it is clear that the applied voltage V leads the current I by an angle ϕ such that

 

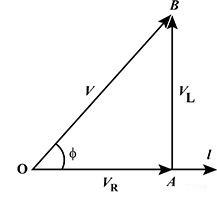
$\tan \phi =\dfrac{{{V}_{L}}}{{{V}_{R}}}=\dfrac{I{{X}_{L}}}{IR}=\dfrac{{{X}_{L}}}{R}=\dfrac{\omega L}{R}$
$\therefore \phi ={{\tan }^{-1}}\left( \dfrac{\omega L}{R} \right)$

Note: - Across inductor voltage leads the electric current.
- Across the resistor the voltage is in phase with electric current.