Question

How do you decide whether or not the equation below has a circle as its graph? If it does, give the centre and the radius. If it does not, describe the graph ~$25x^{2} +25y^{2} -30x+30y-18=0$?

Answer 1

Hint: This given question is based on the equation of the circle. Before solving this, we need to know what the equation of circle? When an arc is drawn from a fixed point, it is called the centre, all points on the curve have the same distance from the centre point of the centre, then a circle is formed. If a circle has a centre and radius, then it will have a graph. Let us solve the problem.

Complete step-by-step answer:
The general form of the equation of any type of circle is represented as
\[ax^{2} +2hxy+by^{2} +2gx+2fx+c=0.................(i)\]
Equation(i) represents the CIRCLE. Only if,
\[(i)a=b\ne 0 (ii)g^{2} +f^{2} -ac>0 \& (iii)h=0\]
So, in this event, its centre $\left(\dfrac{-g}{a} ,\dfrac{-f}{a} \right)$ and radius is $\dfrac{\sqrt{g^{2} +f^{2} -ac} }{\left|a\right|} $
Let consider the given equation of the circle,
\[25x^{2} +25y^{2} -30x+30y-18=0................(ii)\]

In the question, they asked to decide whether the given equation has a circle or not as its graph. To decide whether the given equation has a circle or not, we should compare equation(ii) with equation (i), then we get;
\[a=25=b\ne 0;\]
\[h=0;\]
\[2g=-30\Rightarrow g=-15;\]
\[2f=30\Rightarrow f=15;\]
\[c=-18;\]
Equation (ii) has a circle, now let’s find out its centre and its radius,
Substitute the corresponding values in the formulae
Centre is \[\left( \dfrac{-g}{a},\dfrac{-f}{a} \right)\]
\[\Rightarrow \] \[\left( \dfrac{-(-15)}{25},\dfrac{-15}{25} \right)=\left( \dfrac{3}{5},\dfrac{-3}{5} \right)\]
Radius =\[\dfrac{\sqrt{{{g}^{2}}+{{f}^{2}}-ac}}{\left| a \right|}\]\[\Rightarrow \]\[\dfrac{\sqrt{{{(-15)}^{2}}+{{(15)}^{2}}-(25)(-18)}}{\left| 25 \right|}\]

\[\Rightarrow \dfrac{\sqrt{900}}{25}=\dfrac{30}{25}=\dfrac{6}{5}\]
Putting all together,
\[25x^{2} +25y^{2} -30x+30y-18=0\]
We have centre as $\left(\dfrac{3}{5} ,\dfrac{-3}{5} \right)$ and radius as $\left(\dfrac{6}{5} \right)$

This is a circle.
Then it will have a graph.
‘Eq1’ represents given equation of the circle
‘A’ represents the centre of the circle (black dot).

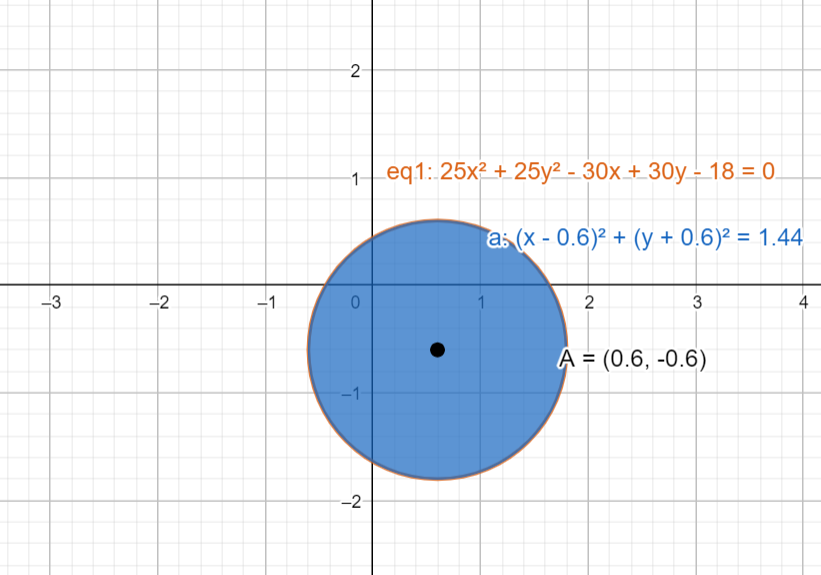
Note: We have alternate method for finding given equation is a circle or not as its graph, i.e., standard form for the equation of the circle
\[\left(x-h\right) ^{2} +\left(y-k\right)^{2} =a^{2} ...............................(iii)\]

Where (h, k) is the centre and ‘a’ is the radius.
Blue region in the graph depicts the equation (iii) form