Question

Curved surface area of a hollow cylinder is $4224c{m^2}$. A rectangular sheet having a width 33 cm is formed cutting it along its height. Find the perimeter of the sheet.

Answer 1

Hint- we will use the formula of the curved surface area of the cylinder in order to find the height of the cylinder. Visualize the sheet as the cylinder in order to find the relationship between the height and length and finally find the perimeter of the sheet.

Complete step-by-step solution -
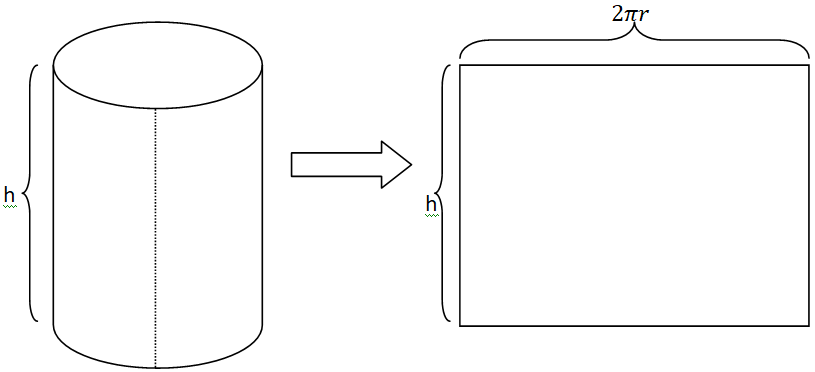
We will solve the problem with the help of the following diagram. This diagram shows the cylinder and further the sheet section of the cylinder after cutting it through its height.
Let for the given cylinder height be h and radius be r,
Now length of the sheet = h and the width of the sheet $ = 2\pi r$
First let us find the equation of curved surface area of the hollow cylinder.
$
   \Rightarrow 2\pi rh = 4224\left[ {{\text{given}}} \right] \\
   \Rightarrow 33 \times h = 4224\left[ {{\text{given in the question}}} \right] \\
   \Rightarrow 33h = 4224 \\
   \Rightarrow h = \dfrac{{4224}}{{33}} \\
   \Rightarrow h = 128cm \\
 $
Now, we have the height of the sheet and the width which is $ = 2\pi r$
Therefore, perimeter of the sheet
$
   = 2\left( {l + w} \right) \\
   = 2\left( {l + 2\pi r} \right) \\
   = 2\left( {128 + 33} \right) \\
   = 2 \times 161 \\
   = 322cm \\
 $
Hence, the perimeter of the sheet is 322 cm.

Note- In order to solve such questions of sectioning of the figure, drawing a figure is a very important part of the solution. Formulas for the surface areas of different figures are also very important and must be remembered, some of them are mentioned above. Try to visualize the problem before starting the solution.