Question

Current ${{I}_{1}}$ in the following circuit is

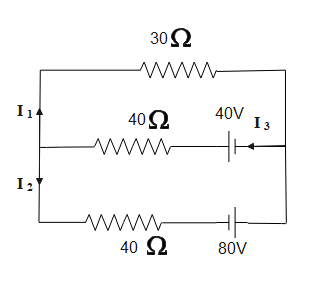
A.0.4 A
B.-0.4A
C.0.8A
D.-0.8A

Answer 1

Hint: We will apply Kirchhoff’s voltage law (KVL) in loop 1 and loop 2. By this we will get two equations having ${{I}_{1}},{{I}_{2}}\text{ }and\text{ }{{I}_{3}}$ .Then applying Kirchhoff’s Current law in one of the junction will give us one equation. Solving all these three equations we will get the value of ${{I}_{1}}$.
Formula: $\sum{V=0}$ and $\sum{I=0}$ in a closed loop.

Complete answer:
For solving such type of questions, we will follow the below steps:
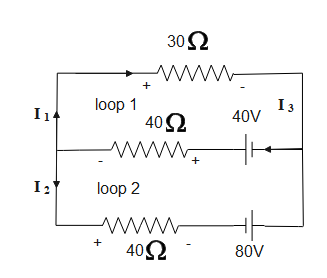
Step 1: Apply KVL in loop 1

$\begin{align}
  & -30{{I}_{1}}+40-40{{I}_{3}}=0 \\
 & \Rightarrow 30{{I}_{1}}+40{{I}_{3}}=40\text{ -----(1)} \\
\end{align}$
Step 2: Apply KVL in loop2
$\begin{align}
  & 40-40{{I}_{3}}-40{{I}_{2}}+80=0 \\
 & 40{{I}_{2}}+40{{I}_{3}}=120 \\
 & \Rightarrow {{I}_{2}}+{{I}_{3}}=3\text{ -----(2)} \\
\end{align}$
Step 3: Apply Kirchhoff’s current law at junction A

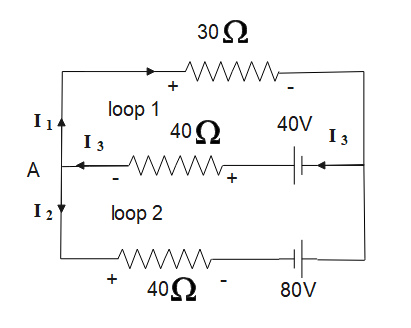
${{I}_{1}}+{{I}_{2}}={{I}_{3}}\text{ -----(3)}$
Now, we will solve equation (1), (2) and (3) we get
$\begin{align}
  & {{I}_{1}}=-0.4A \\
 & {{I}_{2}}=1.7A \\
 & {{I}_{3}}=1.3A \\
\end{align}$
Hence, we got,${{I}_{1}}=-0.4A$

Therefore, Option(B) is correct.

Additional information:
Kirchhoff’s voltage law states that for a closed loop series path the algebraic sum of all the voltages around any closed loop in a circuit is equal to zero.
$\sum{V=0}$
The term “algebraic sum” refers to taking the polarities of the sources and voltage drops around the loop.
Voltage drop in a resistor is given by V=IR
This idea by Kirchhoff is commonly known as the Conservation of Energy
Kirchhoff’s current law states that for a parallel path the total current entering a circuit junction is exactly equal to the total current leaving the same junction. $\sum{I=0}$

Note:
Proper sign convention should be followed while writing KCL and KVL equations. If the direction of current is not given in the question then we can assume it and further solve the question. Voltage drop in a resistor is considered to be negative as shown in the figure.