Question

How many cubic centimetre of iron is required to construct an open box, whose external dimensions are 36cm, 25cm, 25cm and 16.5cm, provided the thickness of the iron is 1.5cm. If one cubic cm of iron weighs 7.5g. Find the weight of the box.

Answer 1

Hint: Find the external volume. Find the internal dimensions of the box. To get the volume of iron used subtract internal volume from external volume. To get the weight of the box we know mass and volume. Thus weight is a product of mass and volume.

Complete step-by-step answer:
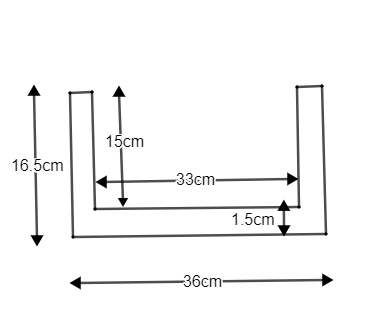
Given us the external dimensions of an open box. Length is given as 36cm, breadth is 25cm and height of the box is given as 16.5cm.

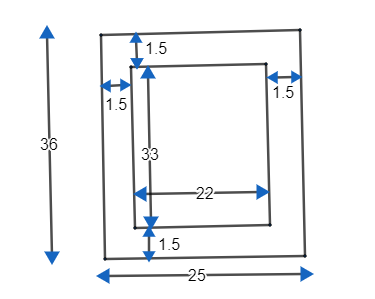
We know the volume of a cube is given by\[lenght\times breadth\times height\]

\[\therefore \]Volume of the box\[=l\times b\times h=36\times 25\times 16.5\]

                                         \[\text{= }14580\text{ }c{{m}^{3}}\]

The thickness of the iron is given as 1.5cm.

We found the volume using the external dimensions. To find the internal dimensions we need to subtract the thickness of iron from the external dimensions.

That is, Internal dimension = External dimension – thickness of iron


\[\begin{align}

  & \text{Internal length = External length - }\left( \text{1}\text{.5 }\!\!\times\!\!\text{ 2}
\right) \\

 & \\

 & \text{ = 36 - }\left( \text{1}\text{.5 }\!\!\times\!\!\text{ 2} \right)\text{ =
33cm} \\

\end{align}\]
\[\begin{align}

  & \text{Internal breadth = External breadth - }\left( \text{2 }\!\!\times\!\!\text{ 1}\text{.5} \right) \\

 & \\

 & \text{ = 25 - }\left( \text{2 }\!\!\times\!\!\text{ 1}\text{.5} \right)\text{ = 22cm} \\

\end{align}\]



\[\begin{align}

  & \text{Internal height = External height - }\left( \text{1}\text{.5} \right) \\
 & \\

 & \text{ = 16}\text{.5 - }\left( \text{1}\text{.5} \right)\text{ = 15cm} \\
\end{align}\]


Thus,


\[\begin{align}

  & \text{Internal Volume = lenght }\!\!\times\!\!\text{ breadth }\!\!\times\!\!\text{ height} \\

 & \\

 & \text{ = 33 }\!\!\times\!\!\text{ 22 }\!\!\times\!\!\text{ 15 = 10890 c}{{\text{m}}^{\text{3}}} \\

\end{align}\]


Thus what we need to find now is the volume of iron used.


\[\begin{align}

  & \text{Volume of iron used = External Volume - Internal Volume} \\

 & \\

 & \text{ = 14850 -10890 = 3960 c}{{\text{m}}^{\text{3}}} \\

\end{align}\]


Given that the weight of 1 \[c{{m}^{3}}\]of iron \[=7.5g\]


\[\begin{align}

  & \text{ }\!\!\backslash\!\!\text{ Weight of the box = Mass }\!\!\times\!\!\text{ Volume} \\
 & \\

 & \text{ = 7}\text{.5 }\!\!\times\!\!\text{
3960=29700g=}\dfrac{\text{29700}}{\text{1000}}\text{kg=29}\text{.7kg} \\

\end{align}\]

Thus, the weight of the box \[29.7kg\].

Note: Read the question carefully. The dimensions provided are the external dimensions. So to get the internal dimension subtract thickness of iron from the external dimension. The most important aim of the question is to find the weight of the box, which you know is the product of mass and the volume of iron used.