Question

What is crystal field splitting energy? How does the magnitude of ${{\Delta }_{0}}$ decide the actual configuration of d orbitals in a coordination entity?

Answer 1

Hint: In presence of ligand field, the metal ions lose their degeneracy of d orbitals and the energy of those d orbitals is connected with crystal field splitting energy. ${{\Delta }_{0}}$ is also known as a crystal field splitting energy or CFSE.

Complete answer:
Whenever ligands approach the metal atom, the d-orbitals of the metal lose its degeneracy and splitting of energy levels happen as a result. Now, the difference between the highly energized energy level and the lowest energy level is called crystal field stabilization energy. It is also called CFSE.
As an example, see the following figure.

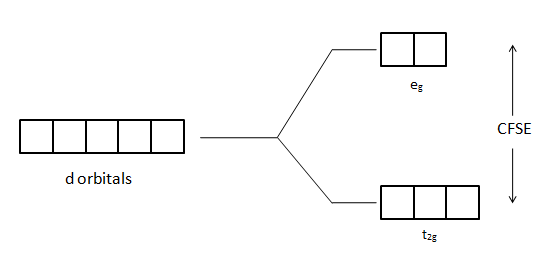
Here, we can see that initially the five orbitals have the same energy. It means that they are degenerated. Then, in the presence of the ligand field, they lose their degeneracy and split into a group of orbitals that have different energies. Different ligand fields have different effects on metals.
- CFSE is also represented by ${{\Delta }_{0}}$. Now the value of pairing energy in the comparison of this CFSE decides the electronic configuration of some metals.
- Now, think of a case where three electrons are there in the three orbitals (${{t}_{2g}}^{3}$)with lower energy. Now the fourth electron can be paired with another electron and it could also be filled in the fourth orbital with higher energy. You can refer to the figure of splitting of orbitals for a better idea.
- If Pairing energy is greater than the CFSE, then the fourth electron will be filled in the orbital with higher energy and no electron will be paired. So, its configuration can be written as ${{t}_{2g}}^{3}{{e}_{g}}^{1}$
- If Pairing energy is lower than the CFSE, then the fourth electron will occupy the orbital having lower energy and will be paired up. The electronic configuration can be written as ${{t}_{2g}}^{4}{{e}_{g}}^{0}$.

Note:
Remember that as P is the pairing energy and ${{\Delta }_{0}}$ being the CFSE, the forthcoming electron will have tendency to be paired when ${{\Delta }_{0}}$ > P and it will have tendency to remain unpaired when
P > ${{\Delta }_{0}}$.