
How do you create a 16 point unit circle that ranges from 0 to 8pi?
Answer
565.2k+ views
Hint: Create the circle of range $\left( 0,2\pi \right)$ instead of $\left( 0,8\pi \right)$ as both are same in case of a circle and $2\pi $is the minimum range for a circle. Plot 16 points by choosing 16 different angles. Choose the angles in such a way that their sine and cosine values are known.
Complete step by step answer:
A circle that ranges from 0 to $8\pi $, is the same as the circle ranges from 0 to $2\pi $because each rotation from one quadrant to another around the coordinate axes is $\dfrac{\pi }{2}$. For a complete circle it will be a complete rotation around 4 quadrants. Hence range will be $\dfrac{\pi }{2}\times 4=2\pi $.
So, to create a circle that ranges from 0 to $8\pi $, we have to create a circle ranging from 0 to $2\pi $.
Now for 16 points we have to consider 16 different angles.
The sine and cosine values of the angles can be taken from the given table
For other angles we just have to change the sign as per the quadrant.
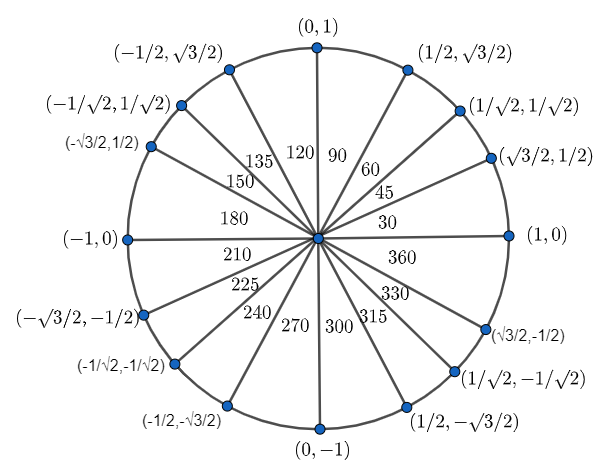
So, the points are
$\begin{align}
& \left( \cos {{0}^{\circ }},\sin {{0}^{\circ }} \right)=\left( 1,0 \right) \\
& \left( \cos {{30}^{\circ }},\sin {{30}^{\circ }} \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right) \\
& \left( \cos {{45}^{\circ }},\sin {{45}^{\circ }} \right)=\left( \dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{60}^{\circ }},\sin {{60}^{\circ }} \right)=\left( \dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{90}^{\circ }},\sin {{90}^{\circ }} \right)=\left( 0,1 \right) \\
& \left( \cos {{120}^{\circ }},\sin {{120}^{\circ }} \right)=\left( -\dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{135}^{\circ }},\sin {{135}^{\circ }} \right)=\left( -\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{150}^{\circ }},\sin {{150}^{\circ }} \right)=\left( -\dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right) \\
& \left( \cos {{180}^{\circ }},\sin {{180}^{\circ }} \right)=\left( -1,0 \right) \\
& \left( \cos {{210}^{\circ }},\sin {{210}^{\circ }} \right)=\left( -\dfrac{\sqrt{3}}{2},-\dfrac{1}{2} \right) \\
& \left( \cos {{225}^{\circ }},\sin {{225}^{\circ }} \right)=\left( -\dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{240}^{\circ }},\sin {{240}^{\circ }} \right)=\left( -\dfrac{1}{2},-\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{270}^{\circ }},\sin {{270}^{\circ }} \right)=\left( 0,-1 \right) \\
& \left( \cos {{300}^{\circ }},\sin {{300}^{\circ }} \right)=\left( \dfrac{1}{2},-\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{315}^{\circ }},\sin {{315}^{\circ }} \right)=\left( \dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{330}^{\circ }},\sin {{330}^{\circ }} \right)=\left( \dfrac{\sqrt{3}}{2},-\dfrac{1}{2} \right) \\
& \left( \cos {{360}^{\circ }},\sin {{360}^{\circ }} \right)=\left( 1,0 \right) \\
\end{align}$
Note:
The angels should be chosen in such a way that their sine and cosine values are known or can be obtained easily. The 16 equal angle difference i.e. $\dfrac{{{360}^{\circ }}}{16}={{22.5}^{\circ }}$should be avoided because there will be complexity in calculation. For sine and cosine values of angles more than ${{90}^{\circ }}$, ASTC rule can be used.
Complete step by step answer:
A circle that ranges from 0 to $8\pi $, is the same as the circle ranges from 0 to $2\pi $because each rotation from one quadrant to another around the coordinate axes is $\dfrac{\pi }{2}$. For a complete circle it will be a complete rotation around 4 quadrants. Hence range will be $\dfrac{\pi }{2}\times 4=2\pi $.
So, to create a circle that ranges from 0 to $8\pi $, we have to create a circle ranging from 0 to $2\pi $.
Now for 16 points we have to consider 16 different angles.
The sine and cosine values of the angles can be taken from the given table
| angle | Cosine value | Sine value |
| ${{0}^{\circ }}$ | 0 | 1 |
| ${{30}^{\circ }}$ | $\dfrac{\sqrt{3}}{2}$ | $\dfrac{1}{2}$ |
| ${{45}^{\circ }}$ | $\dfrac{1}{\sqrt{2}}$ | $\dfrac{1}{\sqrt{2}}$ |
| ${{60}^{\circ }}$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt{3}}{2}$ |
| ${{90}^{\circ }}$ | 1 | 0 |
For other angles we just have to change the sign as per the quadrant.
So, the points are
$\begin{align}
& \left( \cos {{0}^{\circ }},\sin {{0}^{\circ }} \right)=\left( 1,0 \right) \\
& \left( \cos {{30}^{\circ }},\sin {{30}^{\circ }} \right)=\left( \dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right) \\
& \left( \cos {{45}^{\circ }},\sin {{45}^{\circ }} \right)=\left( \dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{60}^{\circ }},\sin {{60}^{\circ }} \right)=\left( \dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{90}^{\circ }},\sin {{90}^{\circ }} \right)=\left( 0,1 \right) \\
& \left( \cos {{120}^{\circ }},\sin {{120}^{\circ }} \right)=\left( -\dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{135}^{\circ }},\sin {{135}^{\circ }} \right)=\left( -\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{150}^{\circ }},\sin {{150}^{\circ }} \right)=\left( -\dfrac{\sqrt{3}}{2},\dfrac{1}{2} \right) \\
& \left( \cos {{180}^{\circ }},\sin {{180}^{\circ }} \right)=\left( -1,0 \right) \\
& \left( \cos {{210}^{\circ }},\sin {{210}^{\circ }} \right)=\left( -\dfrac{\sqrt{3}}{2},-\dfrac{1}{2} \right) \\
& \left( \cos {{225}^{\circ }},\sin {{225}^{\circ }} \right)=\left( -\dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{240}^{\circ }},\sin {{240}^{\circ }} \right)=\left( -\dfrac{1}{2},-\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{270}^{\circ }},\sin {{270}^{\circ }} \right)=\left( 0,-1 \right) \\
& \left( \cos {{300}^{\circ }},\sin {{300}^{\circ }} \right)=\left( \dfrac{1}{2},-\dfrac{\sqrt{3}}{2} \right) \\
& \left( \cos {{315}^{\circ }},\sin {{315}^{\circ }} \right)=\left( \dfrac{1}{\sqrt{2}},-\dfrac{1}{\sqrt{2}} \right) \\
& \left( \cos {{330}^{\circ }},\sin {{330}^{\circ }} \right)=\left( \dfrac{\sqrt{3}}{2},-\dfrac{1}{2} \right) \\
& \left( \cos {{360}^{\circ }},\sin {{360}^{\circ }} \right)=\left( 1,0 \right) \\
\end{align}$

Note:
The angels should be chosen in such a way that their sine and cosine values are known or can be obtained easily. The 16 equal angle difference i.e. $\dfrac{{{360}^{\circ }}}{16}={{22.5}^{\circ }}$should be avoided because there will be complexity in calculation. For sine and cosine values of angles more than ${{90}^{\circ }}$, ASTC rule can be used.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

A solution of a substance X is used for white washing class 11 chemistry CBSE

Differentiate between calcination and roasting class 11 chemistry CBSE




