Question

Coordination number of $C{s^ + }$ and $C{l^ - }$ in $CsCl$ crystal are:
A. $8,8$
B. $4,4$
C. $6,6$
D. $8,4$

Answer 1

Hint: All crystal lattices are built up of repeating unit cells, and in a unit cell, an atom's coordination number is referred to the number of atoms it is touching or in direct contact with or the number of ions that surrounds an ion of the opposite charge within a crystal lattice. For example: In the bcc lattice the coordination number of the corner atoms is eight and the coordination number of the body-center atom is also eight.

Complete answer:
Before calculating the coordination number of $CsCl$ lattice first we need to know the type of unit cell it has and the cesium ions in $CsCl$ forms the simple cubic arrangement and the chloride ions occupy the interstitial sites or is present at the center of the lattice, It can be vice-versa as well that the cesium ions occupy the center of the lattice and the chloride ions show the simple cubic arrangement.
Hence, the center ion is the $C{s^ + }$ ion which is surrounded or directly touching the eight $C{l^ - }$ ions present at the corners of the cube. Similarly, each $C{l^ - }$ ion present at the corners is also surrounded by or directly touching to the eight $C{s^ + }$ ions present at the center of the surrounding unit cells. Thus, the coordination numbers in this type of crystal are both $8$.  This can be easily explained with the help of a diagram as follows:

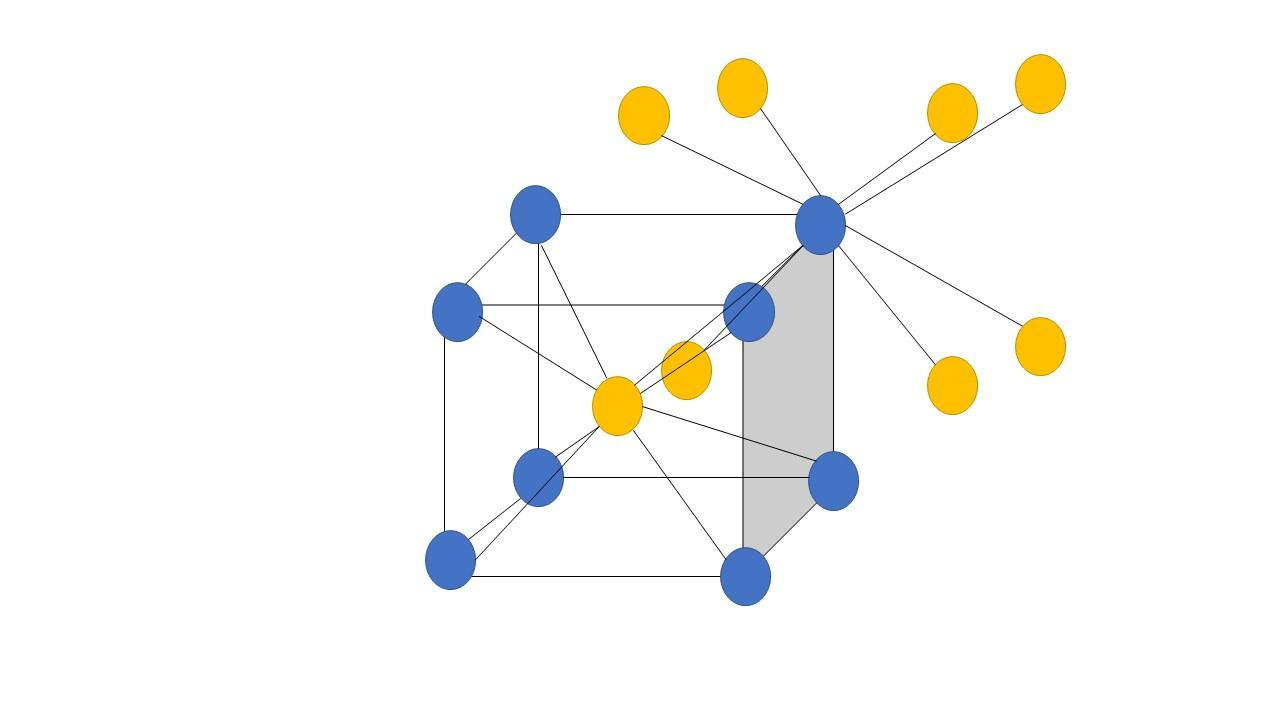
Where the yellow atoms are the ones that are present at the body center which is connected to eight blue atoms or the corner atoms, similarly the blue atoms or the corner atoms are connected to eight yellow atoms or the body center atoms.

Therefore, the correct answer is $8,8$ (Option A).

Note:A student may confuse about that why $CsCl$ is not a body-centered lattice as one of the ions sits at the body center and the other at the corner well this is because for a lattice to be body-centered it requires the same ion to occupy the corners and the center of the lattice.