Question

How do you convert $ r=4\cos \left( \theta \right) $ into rectangular form?

Answer 1

Hint: here, we are asked to convert the equation given in polar coordinates $ \left( r,\theta \right) $ into an equation in rectangular coordinates (x,y). Basically, we need to convert polar coordinates into rectangular coordinates. Completing the square method and Pythagoras theorem is also used in this question.
Use the following formulae for the conversion:
 $ \begin{align}
  & \Rightarrow x=r\cos \theta \\
 & \Rightarrow y=r\sin \theta \\
 & \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=r \\
 & \Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right) \\
\end{align} $
According to Pythagoras theorem:
 $ {{\left( hypotenuse \right)}^{2}}={{\left( perpendicular \right)}^{2}}+{{\left( base \right)}^{2}} $

Complete step by step answer:
Now, let’s solve the question.

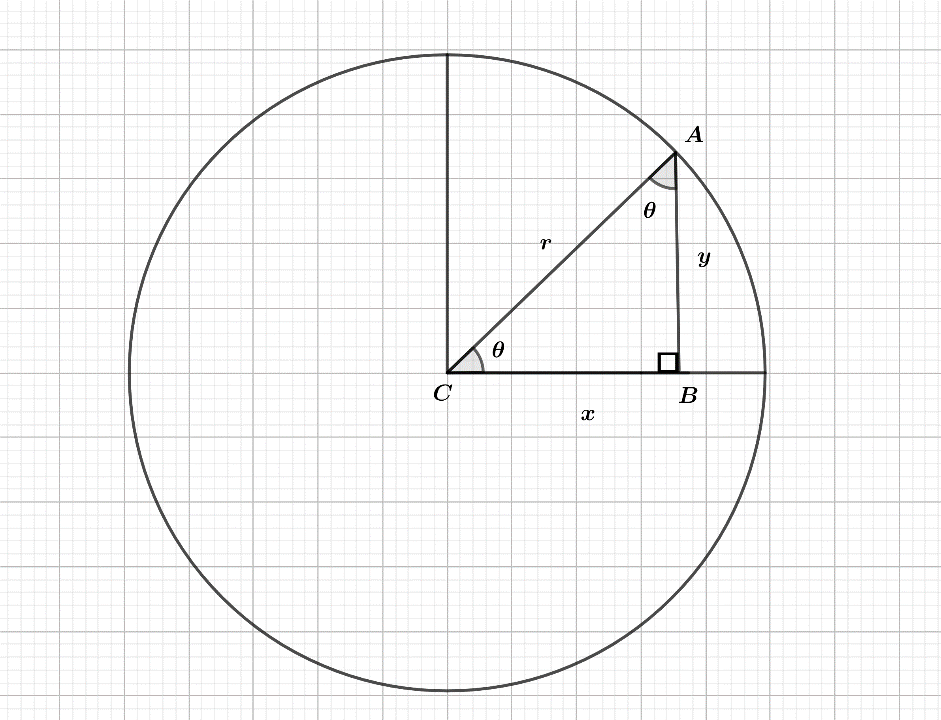
From figure, we can say that the angle formed on the x-axis will be $ r\cos \theta $ and similarly, angle form on the y-axis will be $ r\sin \theta $ . So we can say that:
 $ \begin{align}
  & \Rightarrow x=r\cos \theta \\
 & \Rightarrow y=r\sin \theta \\
\end{align} $
And by using Pythagoras theorem:
 $ \begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}={{r}^{2}} \\
 & \Rightarrow \sqrt{{{x}^{2}}+{{y}^{2}}}=r \\
\end{align} $
The measure of angle $ \theta $ will be: $ \theta ={{\tan }^{-1}}\left( \dfrac{y}{x} \right) $ .
Our given equation is:
 $ \Rightarrow r=4\cos \left( \theta \right) $
Now, multiply both sides with ‘r’. we get:
 $ \begin{align}
  & \Rightarrow r\times r=r\times 4\cos \left( \theta \right) \\
 & \Rightarrow r\times r=4r\cos \left( \theta \right) \\
\end{align} $
As we know $ x=r\cos \theta $ . Now substitute the value of x in above equation. We get:
 $ \Rightarrow {{r}^{2}}=4\times x $
And we also know that $ \Rightarrow {{x}^{2}}+{{y}^{2}}={{r}^{2}} $ . Now substitute this also in above equation. We get:
 $ \Rightarrow {{x}^{2}}+{{y}^{2}}=4x $
On further solving:
 $ \begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}-4x=0 \\
 & \Rightarrow {{x}^{2}}-4x+{{y}^{2}}=0 \\
\end{align} $
Now by completing the square method, add 4 on both the sides of the equation formed above. We get:
 $ \Rightarrow {{x}^{2}}-4x+4+{{y}^{2}}=0+4 $
Now we can see that $ {{x}^{2}}-4x+4 $ can be factorised as $ {{\left( x-2 \right)}^{2}} $ . So place the factors in the equation. We get:
 $ \Rightarrow {{\left( x-2 \right)}^{2}}+{{y}^{2}}=4 $
So, $ r=4\cos \left( \theta \right) $ in rectangular form is $ {{\left( x-2 \right)}^{2}}+{{y}^{2}}=4 $ .

Note:
The main point that should keep in mind is that you need to factorize in the end. You can also see that in the end, the radius in the answer is $ \sqrt{4}=2 $ . ‘r’ needs to be multiplied in the first step, because without it you cannot proceed further.