Question

Convert ${{40}^{\circ }}{{20}^{'}}$ into radian. \[\]

Answer 1

Hint: We recall the definitions of degree and radian as the units to measure angles. We use the formula $R=\dfrac{\pi D}{180}$ to convert from degree to radian where D is the measure of angle in degree and R is the measure of angle in radian.

Complete step-by-step answer:
We know that degree is a unit for measurement of angle in a plane . If D is the measurement of the angle and it is denoted in degree with a small circle superscript $'\circ '$ as ${{D}^{\circ }}$. One degree is equal to the angle subtended at the centre by an arc of length equal to $\dfrac{1}{360}$ of circle. A degree is further divided into minutes and seconds. 1 degree is equal to 60 minutes and 1minuite is equal to 60 seconds. \[\]

We also know that radian is the standard unit for measurement of angle in plane. If R is the measurement of the angle and it is denoted in radian with a small ‘c’ superscript symbol as ${{R}^{c}}$.1 radian is equal to the measure of angle made at the centre of a circle by an arc whose length is equal to the radius of the circle.\[\]

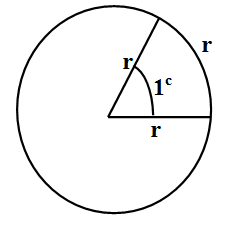
We convert the equal measures ${{R}^{c}}$ and ${{D}^{\circ }}$into other units using fowling formulae.
\[\begin{align}
  & {{D}^{\circ }}=\dfrac{180}{\pi }\times {{R}^{c}} \\
 & {{R}^{c}}=\dfrac{\pi }{180}\times {{D}^{\circ }} \\
\end{align}\]
We are asked to convert the given measure of an angle in degree ${{40}^{\circ }}{{20}^{'}}$ into radian. Let us first convert the given measure in degree and minutes into fractions.
We know that ${{60}^{'}}$ minute is ${{1}^{\circ }}$, then ${{1}^{'}}$ is ${{\left( \dfrac{1}{60} \right)}^{\circ }}$ and then ${{20}^{'}}$ in degree is ${{\left( 20\times \dfrac{1}{60} \right)}^{\circ }}={{\left( \dfrac{1}{3} \right)}^{\circ }}$. So the measure ${{40}^{\circ }}{{20}^{'}}$ in fraction is ${{40}^{\circ }}+{{\left( \dfrac{1}{3} \right)}^{\circ }}={{\left( \dfrac{120+1}{3} \right)}^{\circ }}={{\left( \dfrac{121}{3} \right)}^{\circ }}$
Now we use the formula for converting degrees into radian where $D=\dfrac{121}{3}$. We have;
 \[{{R}^{c}}=\dfrac{\pi }{180}\times {{D}^{\circ }}=\dfrac{\pi }{180}\times \dfrac{121}{3}={{\left( \dfrac{121}{540}\pi \right)}^{c}}\]
The measure of angle in radian is ${{\left( \dfrac{121}{540}\pi \right)}^{c}}$.\[\]

Note: We have used the unitary method for direct variation to convert ${{20}^{'}}$ into degree. We note that a circular angle or complete angle is measured in ${{360}^{\circ }}$ or $2{{\pi }^{c}}$. So we use unitary method for direct variation we have ${{360}^{\circ }}=2{{\pi }^{c}}\Rightarrow {{1}^{\circ }}={{\left( \dfrac{\pi }{180} \right)}^{c}},{{360}^{\circ }}=2{{\pi }^{c}}\Rightarrow {{1}^{c}}={{\left( \dfrac{180}{\pi } \right)}^{\circ }}$ . Another unit of measure of angle is gradians (gons) which measures the complete angle as ${{400}^{g}}$.