Question

Construct the following angles and verify by measuring them by a protractor (i)${75^ \circ }$ (ii)${105^ \circ }$ (iii)${135^ \circ }$

Answer 1

Hint: First draw angles of ${60^ \circ }$ and ${120^ \circ }$then angle bisector between these two angles will be of ${90^ \circ }$ .Draw angle bisector between angles of ${90^ \circ }$ and ${60^ \circ }$ .

Complete step-by-step solution
(i)
1. Draw a ray OA.
2. Taking O as centre and any radius, draw an arc cutting OA at B.

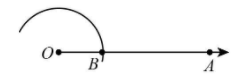
 3. Now, with B as centre and same radius as before, draw an arc intersecting the previously drawn arc at point C.
4. With C as centre, and same radius, draw another arc intersecting the previously drawn arc at point D.
5. Draw ray OE passing through C and ray OF passing through D.

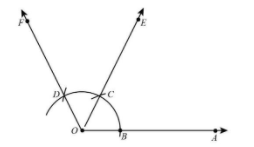
Thus, $\begin{array}{l}
\angle AOE = {60^ \circ }\\
{\rm{and}}\;\angle EOF = {60^ \circ }
\end{array}$
Now, bisect angle EOF twice to get an angle of ${15^ \circ }$
6. Taking C and D as centre, with radius more than half of CD, draw arcs intersecting at P.
7. Join OP.

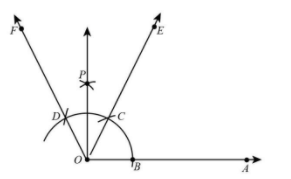
Thus, $\angle EOP = {30^ \circ }$
Mark point Q where OP intersects the arc.
8. Taking Q and C as centres with radius more than half of QC, draw arcs intersecting at R.
9. Join OR

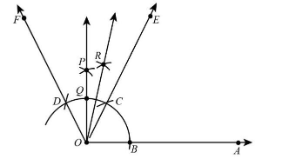
Thus, $\angle AOR = {75^ \circ }$
On measuring the angle AOR by protractor, we find that $\angle AOR = {75^ \circ }$
Thus, the construction is verified.

(ii)${105^ \circ }$
1. Draw a ray OA.
2. Taking O as centre and any radius, draw an arc cutting OA at B.

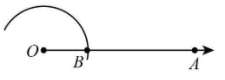
 3. Now, with B as centre and same radius as before, draw an arc intersecting the previously drawn arc at point C.
4. With C as centre, and same radius, draw another arc intersecting the previously drawn arc at point D.
5. Draw ray OE passing through C and ray OF passing through D.

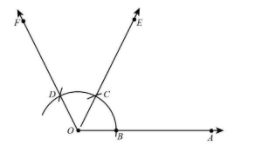
Thus, $\begin{array}{l}
\angle AOE = {60^ \circ }\\
{\rm{and}}\;\angle EOF = {60^ \circ }
\end{array}$
Now, bisect angle EOF twice to get an angle of ${15^ \circ }$
6. Taking C and D as centre, with radius more than half of CD, draw arcs intersecting at P.
7. Join OP.

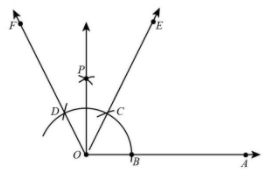
Thus, $\angle POD = {30^ \circ }$
Mark point Q where OP intersects the arc.
8. Taking Q and C as centres with radius more than half of QC, draw arcs intersecting at R.
9. Join OR

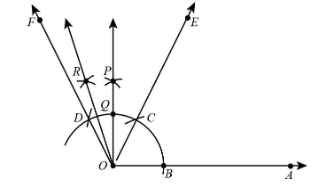
Thus, $\angle AOR = {105^ \circ }$
On measuring the angle AOR by protractor, we find that $\angle AOR = {105^ \circ }$
Thus, the construction is verified.

(iii)${135^ \circ }$
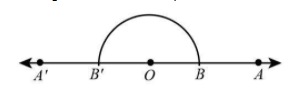
1. Draw a line A’OA.
2. Taking O as centre and any radius, draw an arc cutting at B.

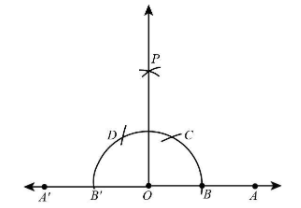
3. Now, with B as centre and same radius as before, draw an arc intersecting the previously drawn arc at point C.
4. With C as centre and the same radius, draw an arc cutting the arc at D.
5. With C and D as centres and radius more than half of CD, draw two arcs intersecting at P.

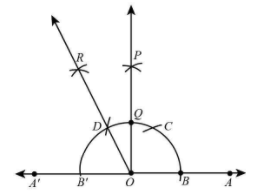
Thus, $\angle AOP = {90^ \circ }$ . Also, $\angle A'OP = {90^ \circ }$ .
So, we bisect$\angle A'OP$ .
Mark point Q where OP intersects the arc.
6. With B’ and Q as centres and radius more than half of B’Q, draw two arcs intersecting at R.
7. Join OR

$\therefore \angle POR = {45^ \circ }$
$\begin{array}{c}
\angle AOR = \angle AOP + \angle POR\\
 = {90^ \circ } + {35^ \circ }\\
 = {135^ \circ }
\end{array}$

Note: In these type of problems ${5^ \circ },{10^ \circ },{20^ \circ },{40^ \circ },{50^ \circ },{70^ \circ },{80^ \circ }$… etc angles cannot be drawn with help of compass.