Question

Construct the angle of $105{}^\circ $ only with the help of a ruler and compass.

Answer 1

Hint: To construct the angle of $105{}^\circ $ we will first draw a ray with the help of a ruler and mark one end of the ray as O. Then, we will draw an arc of any radius by placing the pointed end of the compass on point O. Let us say that the arc cuts the ray at point A, then we will place the pointed end of compass on A and mark angle $60{}^\circ $and $120{}^\circ $ on the arc to get $90{}^\circ $. Now, we will find the bisector of the angle $90{}^\circ $and $120{}^\circ $. Bisectors of the angle $90{}^\circ $ and $120{}^\circ $ are equal to $105{}^\circ $.

Complete step-by-step solution
We will follow the following steps to construct the angle of $105{}^\circ $.
Step1: At first, we will first draw a ray OX and then put the pointed end of the compass at A and draw an arc of any radius which cuts AB at C.

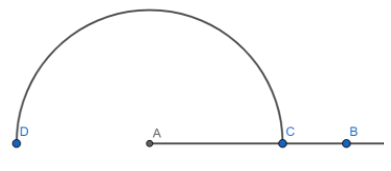
Step2: Now, we will mark the angle of $60{}^\circ $ by putting the compass needle at C and radius equal to the previous arc radius and name it as E. Similarly, now we will mark the point F on the arc CEGFD which makes an angle of $120{}^\circ $ from ray AB.

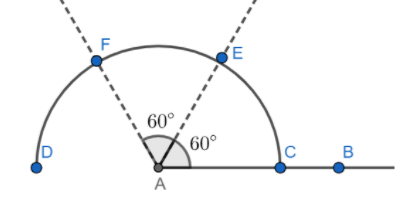
Step3: Now, we will bisect the angle $\angle EAF$ to plot $90{}^\circ $ and then join point G to A to get line AG

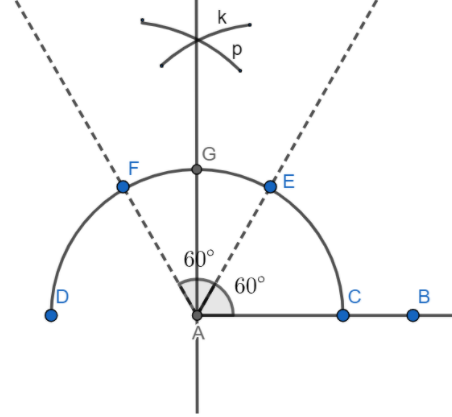
Step4: Now, at last we will see that $\angle FAG$ is equal to $30{}^\circ $, and we also know that $105{}^\circ $ is $15{}^\circ $ahead of $90{}^\circ $. So, we will draw the bisector of $\angle FAG$ just by fixing the radius of the compass and at first, put the needle end of the compass at point G and draw the arc e and the similarly put the needle end at point F and draw the arc d of the same radius as the radius of previous arc e. And at last, we will join the point of their intersection to A. Hence, we will get the required angle i.e. $\angle HAC$= $105{}^\circ $.

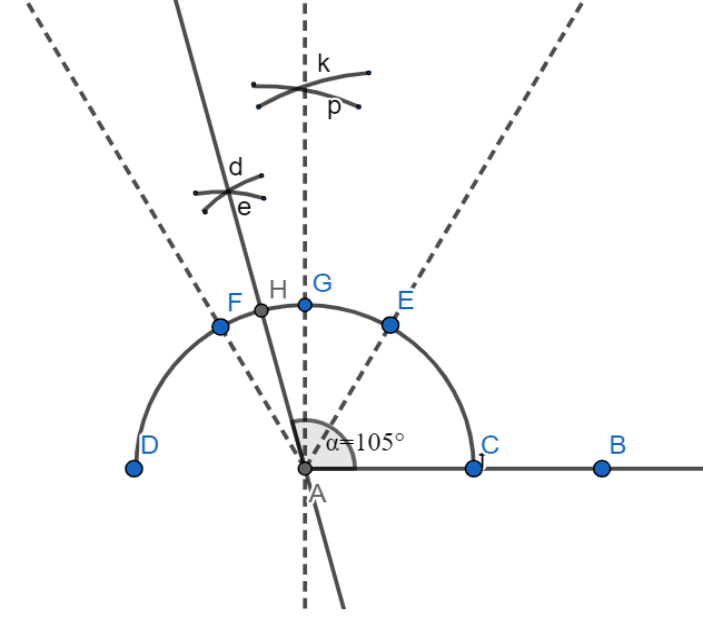
Note: Students are required to follow each step as stated above carefully otherwise they will not get the perfect angle and also note that we can draw the arc CEGFD of any radius. But, after that to mark angle $60{}^\circ $and $120{}^\circ $we have to keep the radius of compass fixed and same as what we have previously taken to draw arc CEGFD, otherwise, we can’t construct an angle of $105{}^\circ $and not even any other angle correctly.