Question

Construct $\sqrt {17} $ on the number line.

Answer 1

Hint: We know that $\sqrt {16} = 4$ and $\sqrt {17} = \sqrt {{4^2} + {1^2}} $. Squaring both sides of the expression and constructing it on a number line. Follow the steps to represent the number on a number line and get the required figure.

Complete step by step answer:
The number system represents the numbers on a number line. Number system is a very useful and important concept in mathematics to represent the numbers on a number line. All types of numbers like natural numbers, whole numbers, rational numbers, Integers are represented on a number line. All the numbers natural numbers, whole numbers, rational numbers, integers are collectively called as real numbers
A number line is a line that serves as an abstraction of real numbers. Every point on a number line is assumed as a real number. The numbers on a number line are placed at equal intervals. According to the question it is given that the number is $\sqrt {17} $.
Here,
$\sqrt {17} $can be written as,
$\Rightarrow \sqrt {17} = \sqrt {{4^2} + {1^2}} $
$\Rightarrow \sqrt {17} = \sqrt {16 + 1} $
Squaring on both sides,
$\Rightarrow {\left( {\sqrt {17} } \right)^2} = {4^2} + {1^2}$
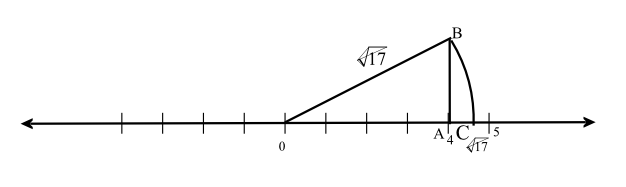
Now, Construct $\sqrt {17} $ on a number line,
Step 1: Draw a number line with equal marks on either side.
Step 2; Consider a point O at zero.
Step 3: Mark a point A at $4$ such that OA is $4$.
Step 4: Construct AB of unit length.
Step 4: Join AB
Step 5: Take OB as radius and intersect the number line at C.
Step 6: Finally, C represents $\sqrt {17} $

Note:
Follow the steps carefully. If you miss any step in constructing the number on a number line, then you will get a wrong answer. A number line can extend infinitely in any direction. The left side of the number line is called the negative side and the right side is called the positive side.