Question

Construct an equilateral triangle, given its side and justify the construction.

Answer 1

Hint: - Here we go through by assuming some length of side of the equilateral triangle. Then for construction of equilateral triangles we use the same length measure by compass for forming the arc. And then join the points where the arc intersects.

Complete step-by-step answer:
Now for constructing the equilateral triangle we first assume the length of the sides of the equilateral triangle.
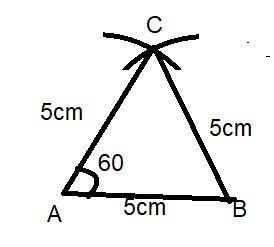
Let us assume that the side of the equilateral triangle is 5cm.
And now for constructing the triangle the steps of constructions are:-
1) Draw a line segment AB of length 5cm.
2) Taking 5cm as radius, and A as center, draw an arc.
3) Taking 5cm as radius, and B as center, draw another arc such that it cuts another arc.
4) Let C be the point where the two arcs intersect.
5) Join AC and BC and label the sides.
By doing these steps we can see that a triangle ABC is formed.
For justification:
By construction, AB = AC = BC (Radius of equal arcs)
And we also check the angles using the protector, we notice that all angles are ${60^0}$.
And we know that by the definition of an equilateral triangle that all the sides are equal and all the interior angles are ${60^0}$.
Hence we can say that $\vartriangle ABC$ is an equilateral triangle.
Note: - whenever we face such a type of construction question for justification and length is not given then assume any length for forming equilateral triangle. And we know that all the sides are equal in equilateral triangle so take the same lengths for forming the other sides. And by completing the construction we can easily verify our answer.