Question

Construct a $\vartriangle STU$ in which $T = {60^ \circ }$, $U = {70^ \circ }$ and $TU = 7.5cm$.

Answer 1

Hint:
This type of problem can be constructed in many ways like we can construct a triangle with the use of a set square or by using a compass also we can construct a triangle. As we all know the sum of an angle in a triangle is ${180^ \circ }$. Therefore for verification after constructing we can measure the third angle and match it.

Complete step by step solution:
First of all we will see the triangle constructed by using the set square.
So the first step will be, we will draw a line segment $TU = 7.5cm$

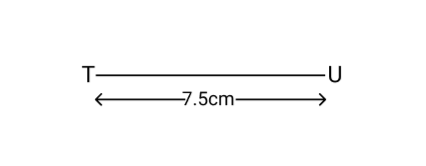
Then we will make an angle ${60^ \circ }$ at the position $T$ by using the set square.

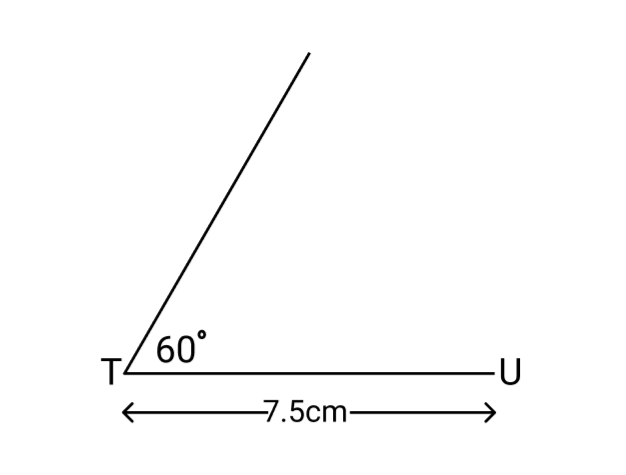
Now we will draw another angle that will be of ${75^ \circ }$ at the position $U$ by using the set square.

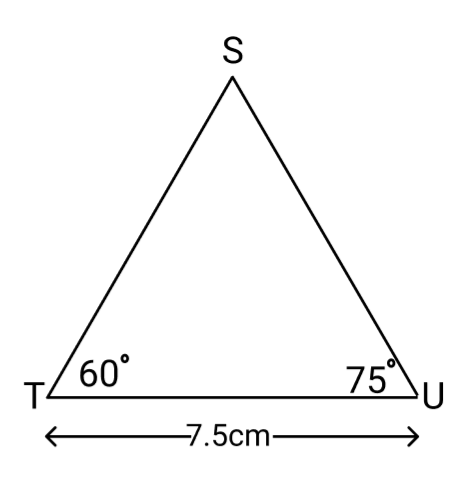
Now we can see that both the angles intersect at the point and we will name it the position $S$.
And in this way $\vartriangle STU$ is constructed.
Now we will see the steps involved while constructing the triangle using the compass.
The first step will be, we will draw a semicircle taking $T$ as the center intersecting $TU$ at $A$ by using the suitable width of the compass.
Then by keeping the compass width the same and we will take $A$ as a center and will cut the semicircle drawn at $B$.
Another step involved will be, we will draw a ray starting from $T$ passing through $B$ has an angle ${60^ \circ }$.
And then utilizing a reasonable width of the compass we will draw a semicircle accepting $U$ as center meeting $TU$ at $C$.
Now keeping compass width the same and accepting $C$ as the focus we will cut half the circle drawn at $D$.
Also keeping compass width the same and accepting $D$ as the focus we will cut half circle further at $E$.
Now utilizing reasonable compass width and taking $D$ and $E$ as focus, we will draw curves converging at $F$. And we will join $UF$ crossing half circle at $G$.
Utilizing appropriate compass width and taking $D$ and $G$ focus we will draw curves converging at $H$. And the last step will be, we will draw a beam beginning from $U$ and going through $H$ has a point${75^ \circ }$.
And in this way, we can construct a$\vartriangle STU$.

Note:
As we have seen the above two methods, the first one is easier and convenient to do as does not require any compass or anything to construct. For the verification, whether the angle we constructed is right or wrong we can check it by adding all the angles of a triangle.