Question

Construct a triangle XYZ in which \[\angle Y = {30^ \circ },\angle Z = {90^ \circ }\,and\,XY + YZ + ZX = 11\,cm\].

Answer 1

Hint:For constructing triangles from the given data, we generally make use of the given congruence conditions and construct the required triangle. Here, in this question, is the base of a triangle, its base angle and sum of the other two sides.

Complete step by step answer:
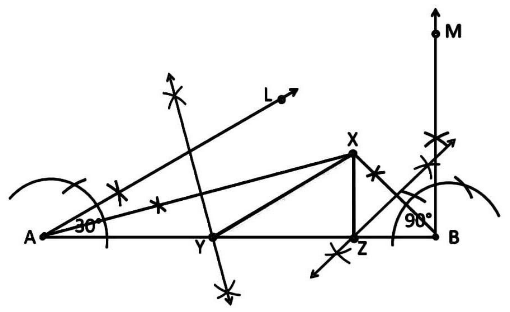
For constructing \[\Delta XYZ\] such that base \[YZ\], base angle \[\angle Y = {30^ \circ }\]and \[\angle Z = {90^ \circ }\], and the sum of other three sides, i.e. \[XY + YZ + ZX = 11\,cm\] are given, the following steps of construction is followed:
Step 1: A line segment \[AB = {\text{ }}11{\text{ }}cm\] is drawn, since \[\left( {XY{\text{ }} + {\text{ }}YZ{\text{ }} + {\text{ }}ZX{\text{ }} = {\text{ }}11{\text{ }}cm} \right)\].
Step 2: An angle, \[\angle A = {30^ \circ }\] is constructed at point \[A\] and an angle \[\angle B = {90^ \circ }\] at point \[B\].
Step 3: \[\angle A\,\,and\,\,\angle B\] are bisected. The bisectors of these angles intersect each other at point \[X\].
Step 4: Perpendicular bisectors \[TS\] of \[AX\] and \[ZU\] of \[BX\] are constructed.
Step 5: Let \[TS\] intersect \[AB\] at \[Y\] and \[ZU\] intersect \[AB\] at \[Z\] further \[XY\] and \[XZ\] are joined. Thus, \[\Delta XYZ\] is the required triangle.

Therefore, such a figure is obtained:

Note:When we are solving any question, which is related to construction, then we should attentively take the markings and measurements, because these things are where we make mistakes and then everything goes wrong. Always remember that your pencil should be sharpened properly, and the compass should be perfectly working without any jerks.