Question

Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \[\dfrac{7}{5}\] of the corresponding sides of the first triangle.

Answer 1

Hint: First of all we will construct a triangle, say \[\Delta ABC\], with sides 5 cm, 6 cm and 7 cm. We will draw a base by taking any of the three sides. Then, we will draw the arc of two sides with the end points of the base as center. To construct a triangle whose sides are \[\dfrac{7}{5}\] of the corresponding sides, we will first draw a ray making an acute angle with the base of the triangle that we constructed and mark 7 points on it.

Complete step-by-step answer:
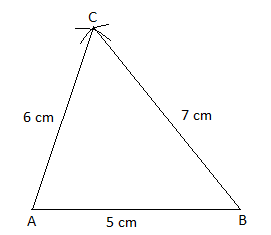
We have been given the sides, 5 cm, 6 cm and 7 cm.
Let us suppose the triangle to be \[\Delta ABC\].
Now we will have to follow the following steps to draw \[\Delta ABC\].
a. We will draw a base of side 5 cm.
b. With A as center and 6 cm as radius, draw an arc.
c. With B as center and 7 cm as radius, draw an arc.
d. Let C be the point where two arcs intersect. Now join AC and BC.
Thus, \[\Delta ABC\] is the required triangle.

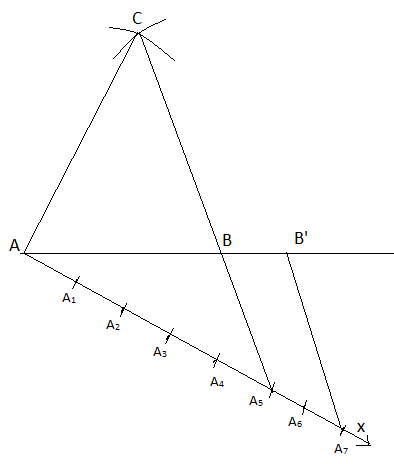
Now, let’s make a similar triangle with scale factor \[=\dfrac{7}{5}\]
We will follow the following steps to make the similar triangle:
a. Draw any ray AX which makes an acute angle with AB.
b. Now we will mark 7 points \[{{A}_{1}},{{A}_{2}},{{A}_{3}},{{A}_{4}},{{A}_{5}},{{A}_{6}},{{A}_{7}}\] on AX such that the adjacent distance is constant.
c. We will join \[{{A}_{5}}B\] and draw a line through \[{{A}_{7}}\] which is parallel to \[{{A}_{5}}B\] to intersect AB extended at B’ as shown below:

d. Now draw a line through B’ parallel to the line BC to intersect AC extended at C’. Thus \[\Delta AB'C'\] is the required triangle.

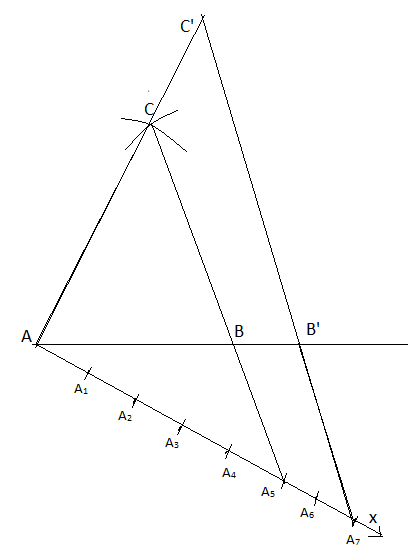
Note: Be careful while taking the points of the ray AX, they should be equidistant at each other. Also, remember that the number of points on the ray is equal to that number which is greater between the numerator and denominator of the scale factor.