Question

Construct a triangle PQR in which $QR = 6\,{\rm{cm}}$, $\angle {\rm{Q = 60}}^\circ $ and ${\rm{PR}} - {\rm{PQ}} = {\rm{2}}\,{\rm{cm}}$.

Answer 1

Hint: In this problem, to construct the triangle PQR use the method of construction of a triangle with one side, one angle and difference of other two sides.

Complete Step-by-step Solution
Given,
One side of the triangle is $QR = 6\,{\rm{cm}}$.
The angle Q is $\angle {\rm{Q = 60}}^\circ $.
The difference between PQ and PO is ${\rm{PR}} - {\rm{PQ}} = {\rm{2}}\,{\rm{cm}}$.

The following are the steps to construct a triangle PQR.

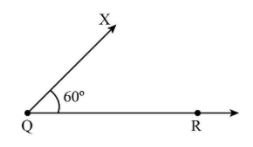
1. Draw the baseline of triangle as $QR = 6\,{\rm{cm}}$.

2. Now, draw an angle of $60^\circ $ from point Q. To make an angle of $60^\circ $, draw a semicircle from point Q and with the same radius of compass intersect this semicircle from point X.

3. Open the compass and fill the distance ${\rm{PR}} - {\rm{PQ}} = {\rm{2}}\,{\rm{cm}}$ and draw an arc from point Q at opposite side of ray QX.

4. Arc intersect ray QX at point D. join point R and D.

5. Now draw a perpendicular bisector of line RD, and extend the line up to ray QX. Mark point P where perpendicular bisector intersects ray QX.

6. Now join PR.

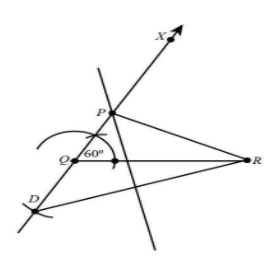
Hence, $\Delta PQR$ is a required triangle.

Note: In such types of problems, while making bisectors of angles remember that radius of compass should be the same to bisect an angle and use a sharp pencil to draw points and to get accurate results.