Question

Construct a triangle PQR if PQ = 5 cm, $\angle PQR={{105}^{\circ }}$ and $\angle QRP={{40}^{\circ }}$.

Answer 1

Hint: In order to solve this question, we will first draw a rough sketch of the triangle which will possibly form an obtuse angle triangle and then by using the protractor, pencil and ruler, we will construct the triangle. Also, we need to remember that the sum of all angles of a triangle is 180˚.

Complete step-by-step solution -
In this question, we have been asked to construct a triangle PQR if PQ = 5 cm, $\angle PQR={{105}^{\circ }}$ and $\angle QRP={{40}^{\circ }}$. To solve this question, we should know that the sum of all the interior angles of a triangle is 180˚. So, for triangle PQR, we can say,
$\angle PQR+\angle QRP+\angle RPQ={{180}^{\circ }}$
Now, we will put the value of $\angle PQR={{105}^{\circ }}$ and $\angle QRP={{40}^{\circ }}$ in the above equation, so we will get,
$\begin{align}
  & {{105}^{\circ }}+{{40}^{\circ }}+\angle RPQ={{180}^{\circ }} \\
 & \angle RPQ={{180}^{\circ }}-{{105}^{\circ }}-{{40}^{\circ }} \\
 & \angle RPQ={{35}^{\circ }} \\
\end{align}$
So, we can say, the triangle will look something like the figure shown below.

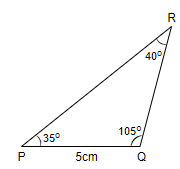
Now, to construct an accurate triangle, we will follow a few steps. So, we get,
Step 1: We will draw a line segment of 5 cm as PQ. So, we get,

Step 2: Now, we will place the center of the protractor over point Q. And we will measure 105˚ from left to right, mark that angle, draw the line and extend it.

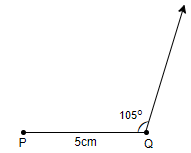
Step 3: Now, we do not know where the point R lies, so we will first draw the angle 35˚ from point P. So, we will place the center of the protractor over the point P, measure an angle of 35˚ from left to right and then we will extend that line so that it meets the line drawn from point Q at a point. And then, we will mark the point where the two lines meet as R. So, we get,

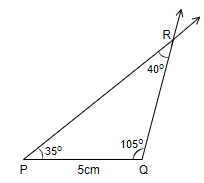
Therefore, we have constructed the triangle PQR for PQ = 5 cm, $\angle PQR={{105}^{\circ }}$ and $\angle QRP={{40}^{\circ }}$.

Note: While solving this question, if we make $\angle QRP$ instead of $\angle RPQ$, then we will probably not get the correct triangle because we do not know the length of QR. What we only have is the length of PQ, so we will probably make those angles which can be formed on the line PQ. Also, after constructing the triangle we can check if the angle QRP is 40˚ to check if our construction is correct or not.