Question

Construct a triangle of sides 4.2cm, 5.1cm and 6cm. Then construct a triangle similar to it, whose sides are $\dfrac{2}{3}$ of corresponding sides of the first triangle.

Answer 1

Hint: To solve this construction question first you have to draw a triangle of given dimensions and then further draw a similar triangle using properties of similar triangles.

Complete step-by-step solution -

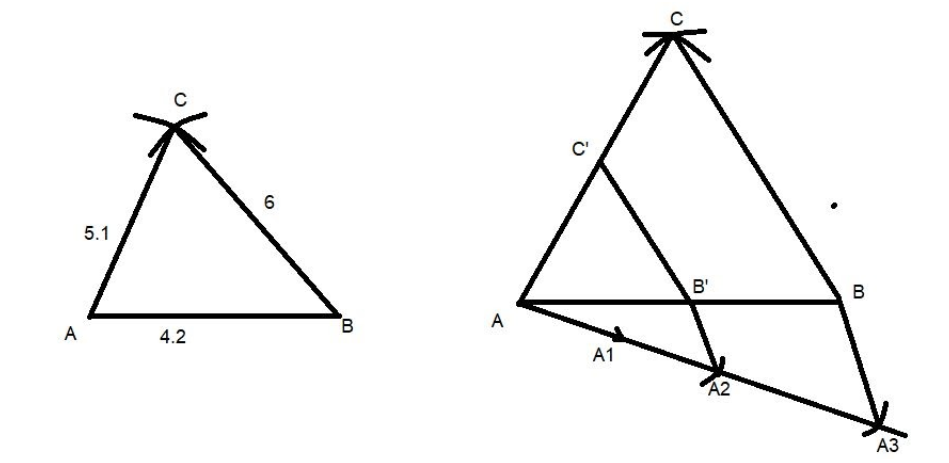
Draw a line segment AB=4.2 cm Draw an arc at 5.1 cm from point A. Draw an arc at 6 cm from point B so that it intersects the previous arc. Joint the point of intersection from A and B. This gives the required ABC.
Dividing the base in 2:3 ratio:
Because we have to draw a similar triangle whose sides are $\dfrac{2}{3}$of corresponding sides of the first triangle.
Draw a ray AX at an acute angle from AB. Plot three points on AX so that; $A{A_1} = {A_1}{A_2} = {A_2}{A_3}$ Join ${A_3}$​ to B.  Draw a line from point A2​ so that this line is parallel to A3​B and intersects AB at point B’. Draw a line from point B’ parallel to BC so that this line intersects AC at point C’.

Note: -Whenever you get this type of question the key concept of solving is you have to construct using the dimension given in the question. You have to divide the base of the first triangle in the ratio 2:3 to get sides of a similar triangle in the 2:3 ratio.