Question

Construct a triangle ABC of side of length AB = 3 cm, BC = 4 cm and AC = 5 cm.

Answer 1

Hint: To solve this question, we will first try to check if the obtained triangle length is a measure of a right-angled triangle. For that, we will check the Pythagoras theorem for the sides of the given triangle. If so, then we will make a right-angled triangle. After obtaining it to be a right-angled triangle, we will first select the base and then follow certain steps of construction to get the result.

Complete step-by-step solution:
We have the sides of a triangle ABC as given below
\[\begin{align}
  & AB=3cm \\
 & BC=4cm \\
 & AC=5cm \\
\end{align}\]
Now, let us state the Pythagoras theorem. It is stated as “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides.” Because AC is of measure 5cm, the largest sides, hence it is the hypotenuse. Using the Pythagoras theorem,
\[{{\left( AC \right)}^{2}}={{\left( 5 \right)}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}}\]
As, \[{{5}^{2}}=25,\] and \[{{3}^{2}}+{{4}^{2}}=9+16=25\]
Hence, the Pythagoras theorem is satisfied.
The above ABC is a right-angled triangle with side AC = 5cm. So, we will construct a right-angled triangle ABC of AC as the hypotenuse. We will consider BC = 4cm as the base and let us do the steps of construction.
Steps of Construction
Step 1: Construct a line of length BC = 4 cm.

Let us draw a 90-degree angle on point B, for that too we will consider the next step of construction.
Step 2: Place the compass on point B and draw an arc on line BC such that a point P is obtained. Now, with the same radius place the compass at point P, draw another arc such that it intersects the previous arc at point E. The below fig shows the details.

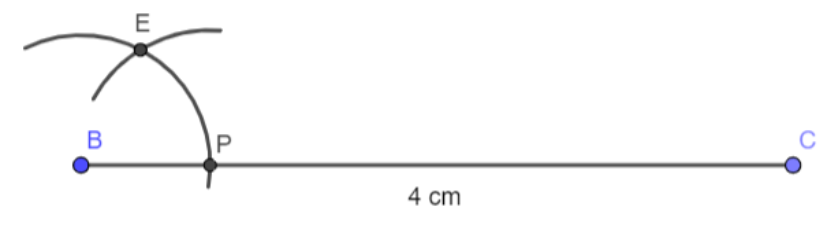
Step 3: Place the compass at E and with the same radius as taken before for drawing an arc and on the previous arc and name it as F.
Also with the same radius on the compass draw an arc above with the compass point once at E and then at F. You will get an intersection of arcs here.

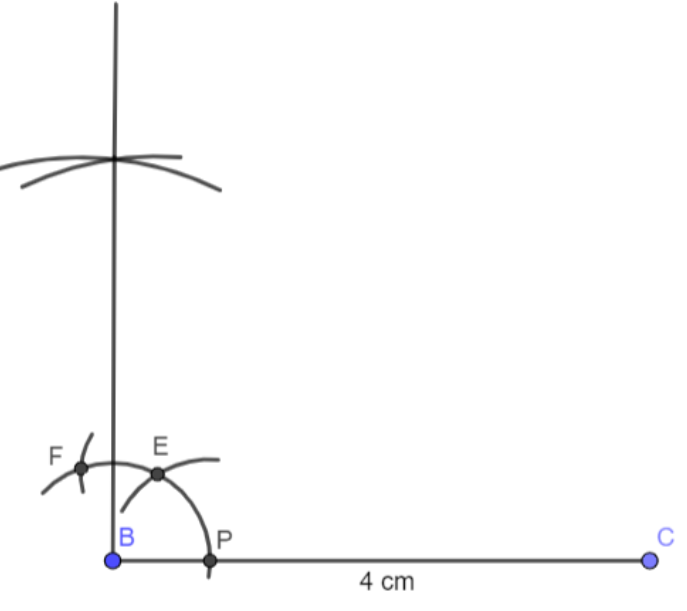
Step 4: Now we need point A on this line. Take the point of the compass on B and length of the compass as 3 cm and draw an arc on this line and name it as A. Join A and C.

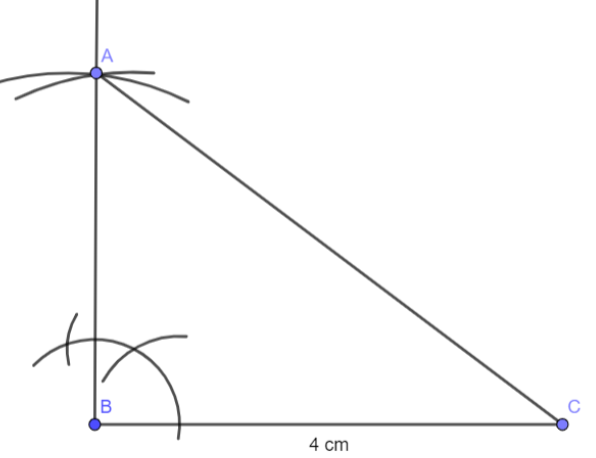
So, this is a right-angled triangle ABC that is formed.

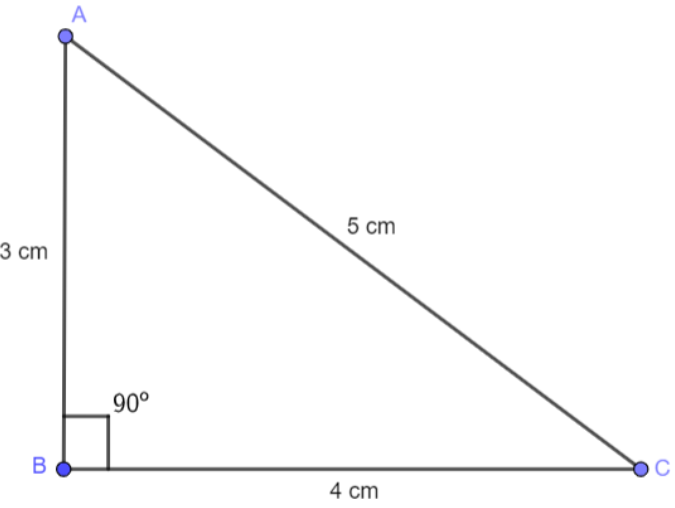
Thus our triangle ABC is formed and it is a right-angled triangle.

Note: The students should not get confused about taking different bases. Even if the base is taken as 3cm, then also the triangle would be the same. The angle of 90 degrees would be made and AC would again be 5cm hypotenuse. So, taking different lines as the base doesn’t matter. The triangle is anyway the same.