Question

Construct a rectangle WXYZ in which \[{\text{WX = 7 cm}}\] and \[{\text{XY = 4 cm}}\]. Find the length of its diagonal.
a) \[\sqrt {65} {\text{ cm}}\]
b) \[\sqrt {64} {\text{ cm}}\]
c) \[\sqrt {56} {\text{ cm}}\]
d) None of these

Answer 1

Hint: A rectangle is a type of quadrilateral in which the length of the opposite sides is equal and each interior angle is a right angle. To solve this question, we will first construct a rectangle according to the given dimensions. Then with the help pythagoras theorem we will find the required answer.

Complete answer:

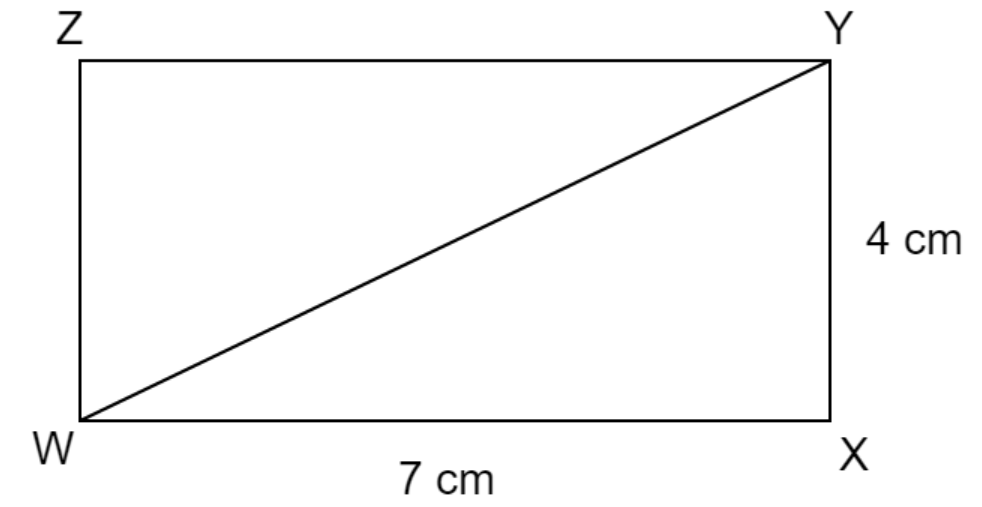
So, the above figure is the rectangle with the given dimension.
We have to find the length of the diagonal that is \[{\text{WY}}\].
We know, \[\angle {\text{WXY = }}{90^ \circ }\]
So, \[\vartriangle {\text{WXY}}\] is a right angled triangle. Therefore, we can apply Pythagoras theorem. So, we have;
\[{\text{W}}{{\text{Y}}^2} = {\text{W}}{{\text{X}}^2} + {\text{X}}{{\text{Y}}^2}\]
On putting the values, we get;
\[ \Rightarrow {\text{W}}{{\text{Y}}^2} = {7^2} + {4^2}\]
\[ \Rightarrow {\text{W}}{{\text{Y}}^2} = 65\]
On simplification we get;
\[ \Rightarrow {\text{WY}} = \sqrt {65} {\text{ cm}}\]
Hence the length of the diagonal is \[\sqrt {65} {\text{ cm}}\].
Therefore, the correct option is A

Additional details:
A crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles and not all equal, though opposite angles are equal.

Note: One important thing to note is that all squares are rectangles but all rectangles are not squares. This is because square have all the sides equal and all the angle equal to ninety degrees. This means that the opposite sides of squares are also equal and this is the property of a rectangle. But in the case of a rectangle , all the sides are not equal, so it cannot be called a square.