Question

Construct a quadrilateral ROAM, where RO = 4cm, OA = 5cm, \[\angle R={{50}^{\circ }},\angle O={{110}^{\circ }}\] and \[\angle A={{70}^{\circ }}\].

Answer 1

Hint: Assume RO as the base of the quadrilateral of length 4cm. Use a protractor to draw an angle of \[{{50}^{\circ }}\] at point R and an angle of \[{{110}^{\circ }}\] at point O. Use scale to mark a length of 5cm from point O on the extended line of angle and name it A. Now, draw an angle of \[{{70}^{\circ }}\] at point A and extend the line to meet the extended line of \[\angle R\] at the point M.

Complete step by step answer:
Here, we have been provided with the following information regarding a quadrilateral ROAM: - RO = 4cm, OA = 5cm, \[\angle R={{50}^{\circ }},\angle O={{110}^{\circ }}\] and \[\angle A={{70}^{\circ }}\]. We have to construct the quadrilateral ROAM. So, follow the following steps to draw the quadrilateral: -
Step 1: - Consider RO as the base of the quadrilateral and construct a line of length 4cm using scale. Mark the endpoints as R and O.

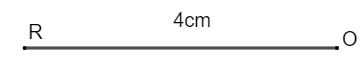
Step 2: - Place a protractor at point R and draw an angle of \[{{50}^{\circ }}\] and extend the line. Similarly, place the protractor at point O and construct an angle of \[{{110}^{\circ }}\] towards the left side and extend the line.

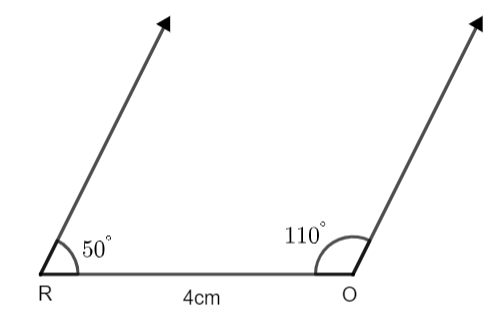
Step 3: - Use scale to mark a point A at a distance of 5cm from O on the extended line.

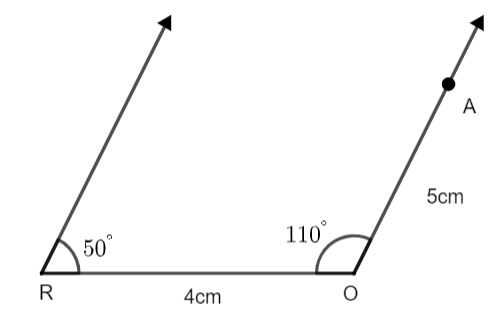
Step 4: - Place the protractor at point A with OA as the baseline of the protractor and draw an angle of \[{{70}^{\circ }}\]. Extend the line to meet the extended line of R at M.

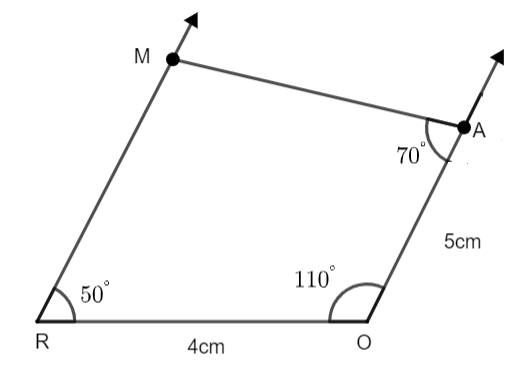
Hence, our quadrilateral ROAM is complete.

Note: One may note that here we have considered RO = 4cm as the base of our quadrilateral. We can also assume the other given side OA = 5cm as the base of our quadrilateral. Remember that two sides are unknown so never assume them as the base. The length of these sides can be calculated by using a scale. The fourth angle can be determined with the help of a protractor or we can subtract the sum of given three angles from \[{{360}^{\circ }}\].