Question

Construct a quadrilateral \[\] LMNO such that l (LM) = l (LO) = 6 cm, l (ON) = l (NM) = 4.5cm, l(OM) = 7.5 cm.

Answer 1

HINT: For solving the questions that involve construction, we have to follow specific steps that are unique to a particular question which might include the construction of some known angles.
The construction of some common angles must be known beforehand as they might be used in these types of questions.

Complete step-by-step answer:
As mentioned in the question, we have to construct a quadrilateral \[\] LMNO.

Now, we will follow the below mentioned steps in a chronological manner to obtain or construct the required quadrilateral.

1) Firstly, we will draw a horizontal line segment LM=6cm.

 2)Now, from point L, we will draw an arc having radius=6cm.

3) Then, from point M, we will draw another arc having radius=7.5cm in such a way that it intersects with the arc that we have drawn in step 2. The point of intersection of these two arcs that are made by us is point O.

4) Now, we will join points LO and OM. LO is the side of the quadrilateral that we are constructing while OM is the diagonal of this quadrilateral which we are constructing.

5) Now, we will draw an arc having radius =4.5cm from point O.

6) From point M, we will then draw another arc having radius=4.5cm such that it intersects with the arc that we have drawn in step 5.The point of intersection is N.

7) On joining points O and N and points M and N, we get ON and MN that are also the sides of quadrilateral \[\] LMNO.

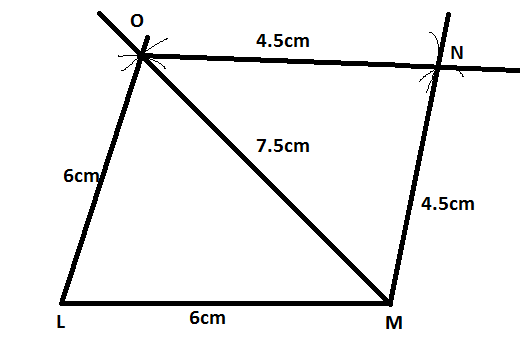
Hence, we obtained the quadrilateral \[\] LMNO.


NOTE: -
The students can make an error if they don’t follow the correct procedure and that too in order because otherwise the students would not get to the right figure as in such questions, following the procedure correctly is very important to get to the correct shape.