Question

Construct a parallelogram ABCD, when AB = 5.8cm, diagonal AC = 8.2cm and diagonal BD = 6.2cm.

Answer 1

Hint: Draw a line segment AB. Take half of AC and BC and cut arc from point A and point C at O. Extend OA and OB to get the given length of diagonal AC and BD. Join all sides to get the parallelogram ABCD.

Complete step-by-step solution -

We need to construct a parallelogram ABCD. We know that in a parallelogram the opposite sides are equal and parallel. Thus we can say that,

AB = DC = 5.8cm.
Similarly, BC = AD.
Now the diagonals of a parallelogram bisect each other, which means that diagonals AC and BD intersect each other at O. Given, AC = 8.2cm, BD = 6.2cm. From the rough figure we have drawn we can say that,
AO = OC and BO = OD.
Therefore, \[AO=\dfrac{AC}{2}=\dfrac{8.2}{2}=4.1\]cm
\[BO=\dfrac{BD}{2}=\dfrac{6.2}{2}= 3.1 \]cm
Now let us first draw the line segment AB of length 5.8cm.
Now let us take A as center and draw an arc of 4.1cm. Similarly, take B as the center and draw an arc of 3.1cm. Now both the arc intersects at the point O.
Now join AO and BO. Extend AO to BO. Extend AO to C such that we get AC = 8.2cm. Similarly extend BO to D and we get BD = 6.2cm.
Finally join BC, CD and DA. Measure three sides and we get the required parallelogram ABCD.

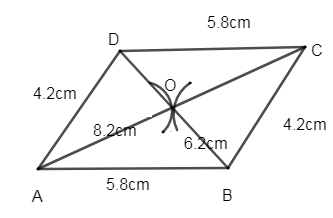
Thus we got the parallelogram ABCD, with AB = DC = 5.8cm and AD = BC = 4.2cm.
Hence we have constructed a parallelogram ABCD.

Note: It is given clearly that 2 length is diagonal. Don’t confuse them and take it as the sides of the parallelogram. Then the entire construction would be wrong. Remember that the diagonals intersect at point O. The basic of drawing a parallelogram is that you know its basic properties.