Question

Construct a parallelogram \[ABCD\] in which \[AB=6.5\text{ }cm,\text{ }AC=3.4\text{ }cm\] and the altitude \[AL\] from $ A $ is \[2.5\text{ }cm\] . Draw the altitude from $ C $ and measure it.

Answer 1

Hint: For constructing a parallelogram first we need to draw a baseline and mark the 2 arcs respectively from the 2 end points of the base line with the radius equal to the required length and draw a ray joining the end point and the arc and mark the point of intersection on arc and join the both points on the arc.

Complete step-by-step answer:
For constructing a parallelogram \[ABCD\] in which \[AB=6.5\text{ }cm,\text{ }AC=3.4\text{ }cm\] and the altitude \[AL\] from $ A $ is \[2.5\text{ }cm\] , we have to follow the below steps one by one.
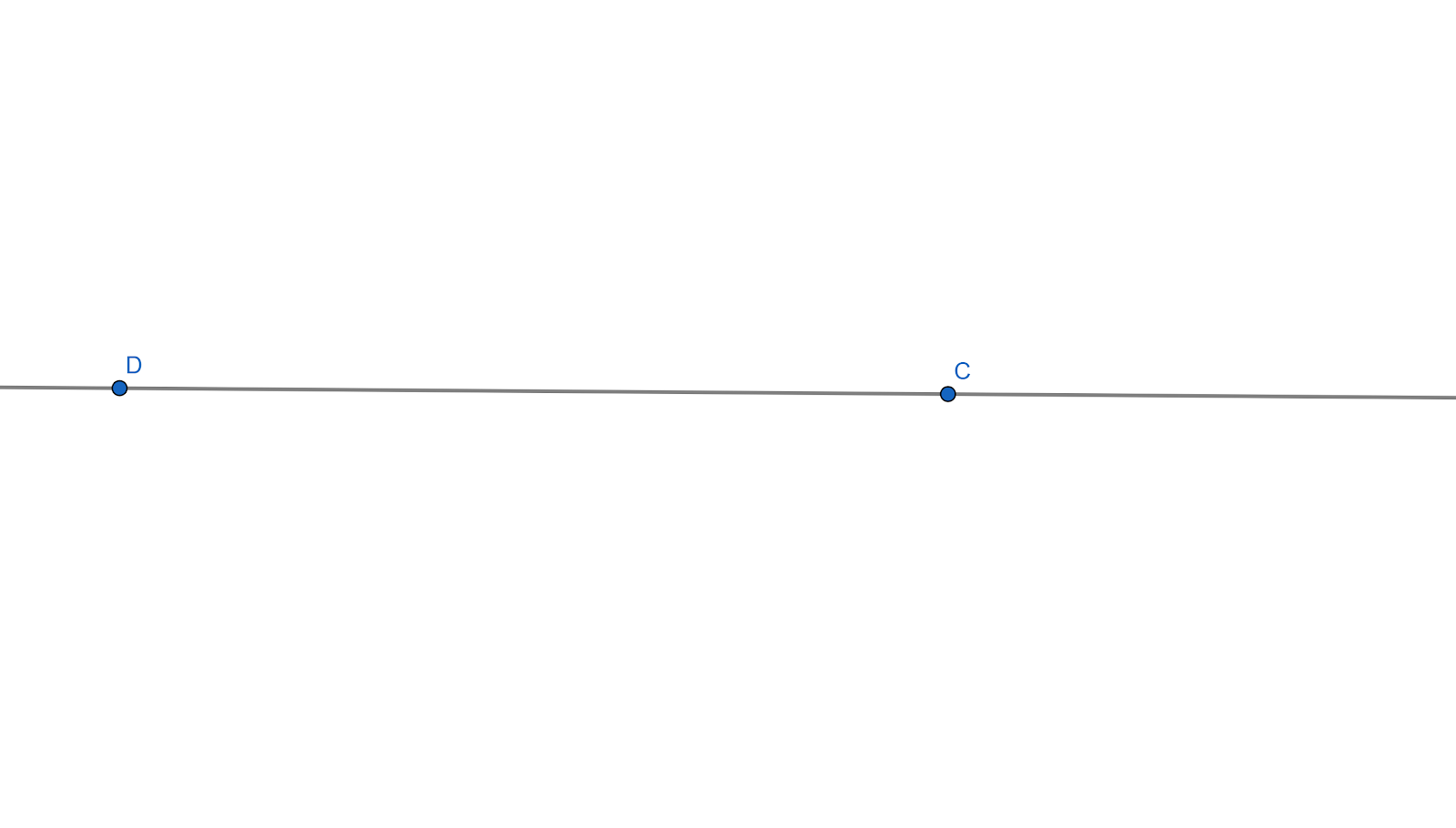
(1) Draw a line $ DC=6.5cm $ as a base line. Since, we know that parallelograms have parallel lines of equal lengths. Here, $ AB $ and $ DC $ are parallel and are of equal length.

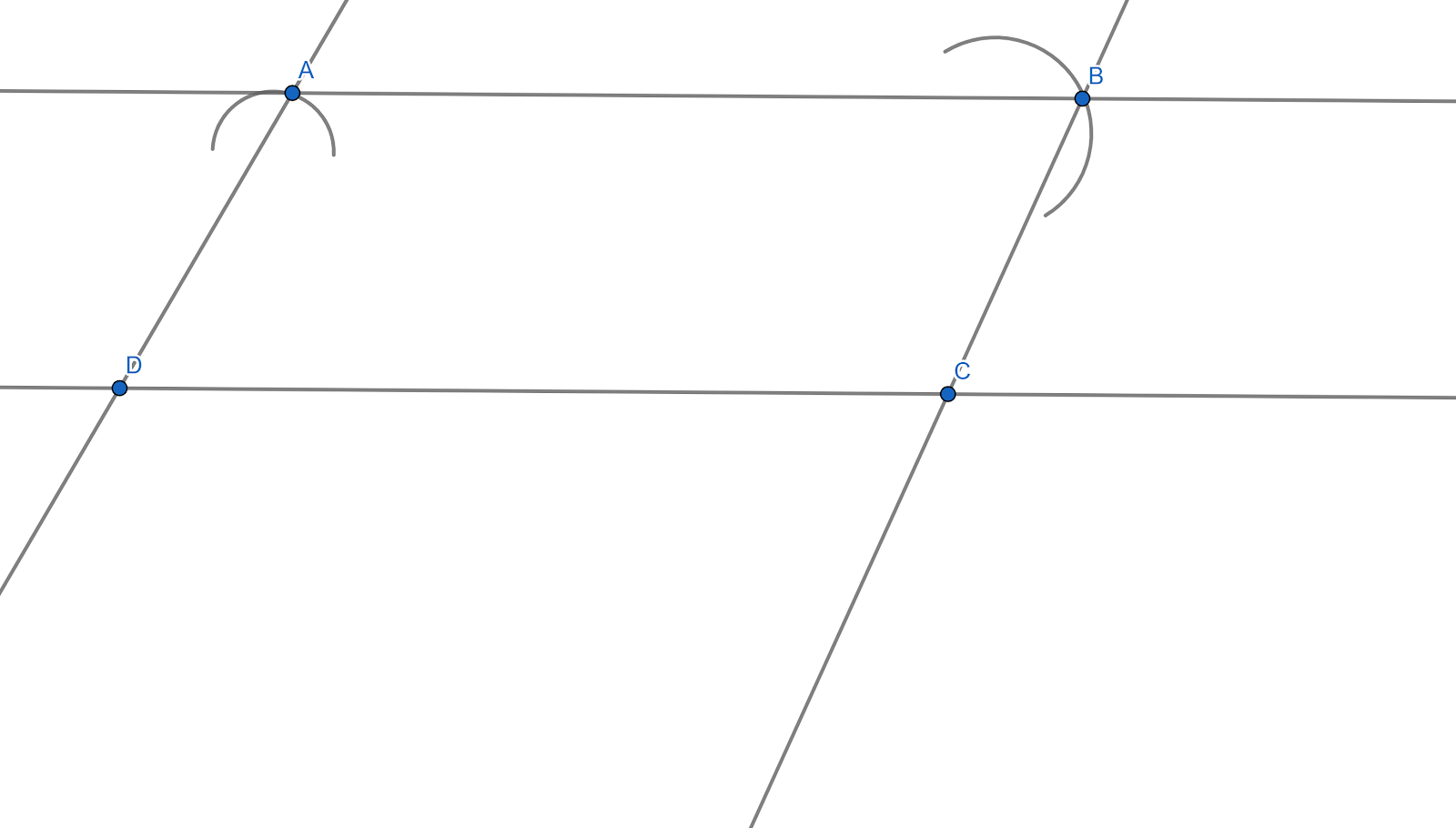
(2) Now with the help of a compass with radius 3.4cm (since the length of \[\text{ }AC=3.4\text{ }cm\] and it will be parallel to the line $ BD $ with equal length), draw 2 arcs from points D and C respectively. Now from point D draw a ray cutting the previous arc and mark it as A and similarly draw a ray from point C and mark it as B. Now join B to C.

(3) Our parallelogram \[ABCD\] is completed.

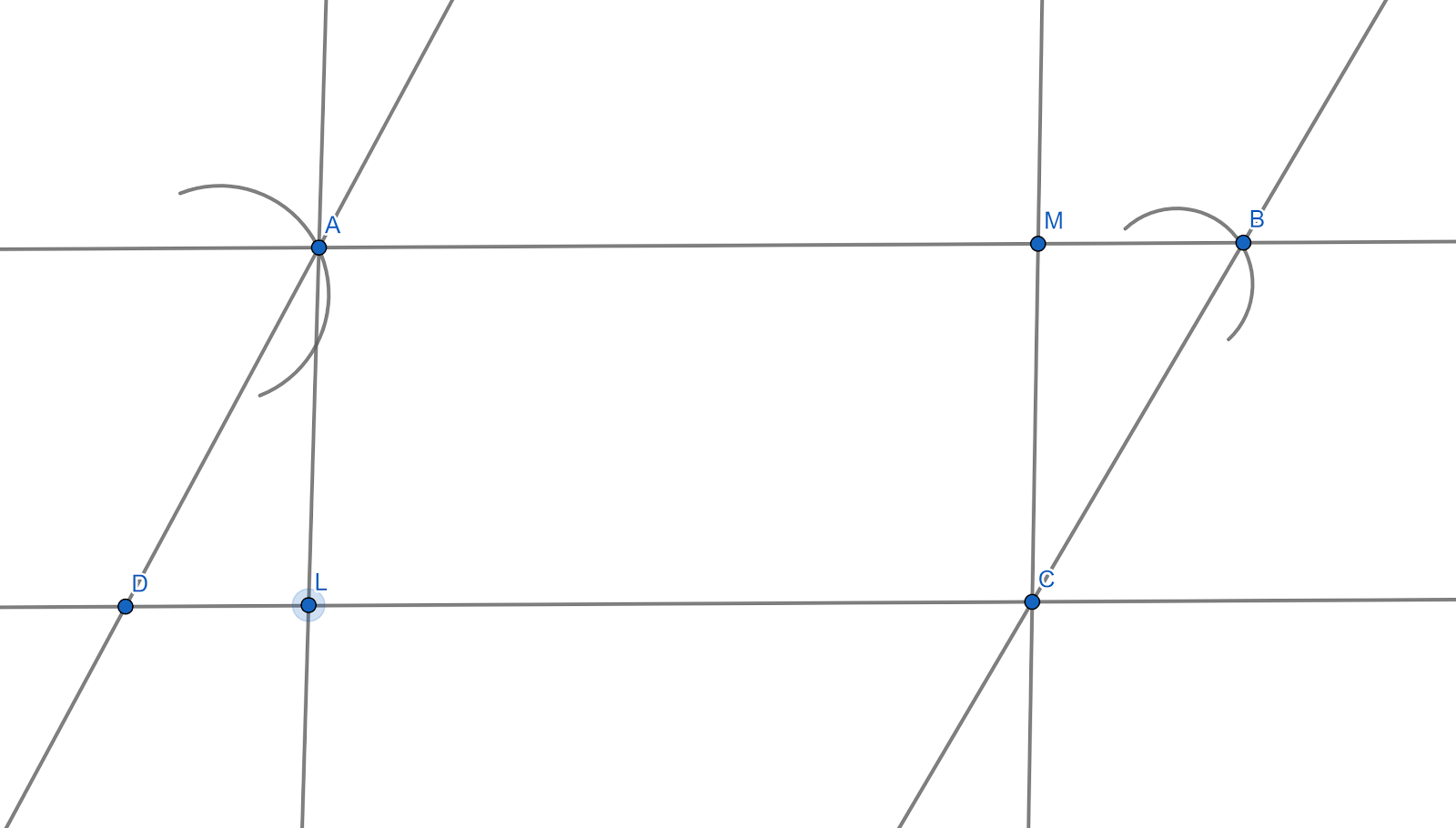
To find the measure of altitude $ CM $ . We should take a compass and a ruler and measure the line $ CM $ it will be equal to \[2.5\text{ }cm\] .
We know that altitudes in parallelograms are parallel and equal. In the question it is given that the altitude \[AL\] from $ A $ is \[2.5\text{ }cm\] .
Therefore, measure of altitude $ CM=2.5cm $ .


Note: Here while drawing the arc using the compass we should be taking the radius carefully. While answering these types of questions we should take care about the lengths given in the question and used during our construction, they should be accurate.