Answer
396.6k+ views
Hint: Here we will draw the required construction step by step. First we draw a circle of radius 5cm and then taking a point 3cm apart as the centre, we will draw another radius of 2cm. Finally at the point of contact of the two circles, we will have an angle of 90 degrees. The line that forms is the tangent.
Complete step-by-step answer:
The steps for making the required construction are as follow:
Step1: Draw a line segment of 3cm
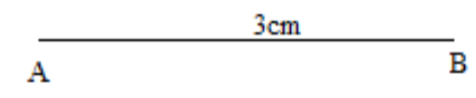
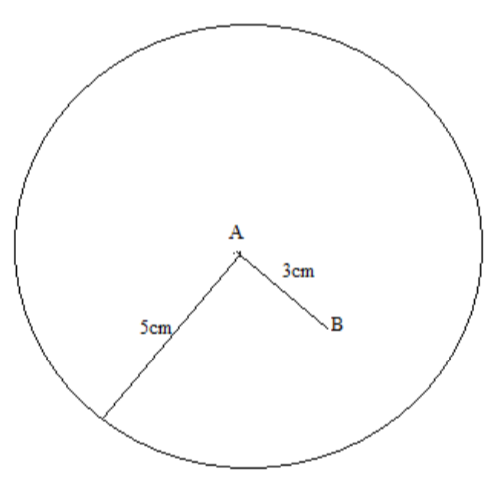
Step2: Then draw a circle of radius 5cm taking as the centre. The circle is drawn using a compass.
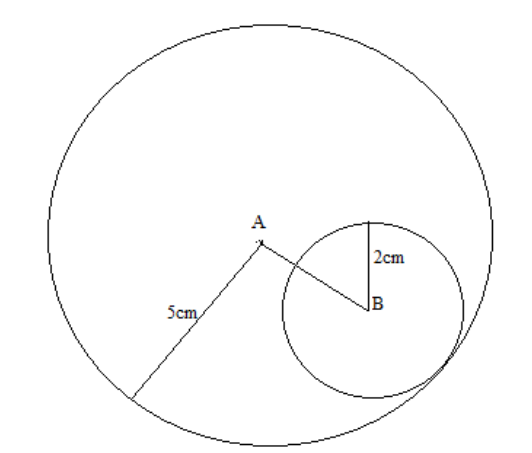
Step3: Now draw another circle of radius 2cm taking B as the centre. Since the distance between the centres is 3cm. So, both the circles will touch at the point P.
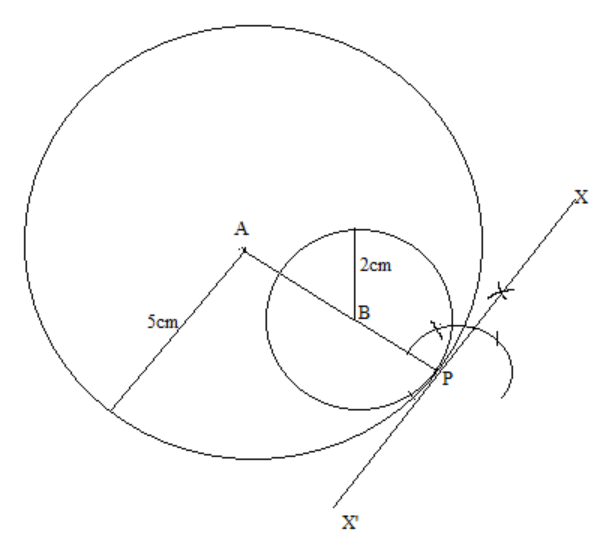
Step4: Now to draw the common tangent, we will make an angle of 90 degree at the common point of the two circles. So, we will join AP and then draw a perpendicular to AP at vertex P.
The perpendicular XX’ formed by joining the two points will be the required common tangent of two circles.
Note In the construction related to the tangent on the circle, the important point is that you should know that the tangent drawn at a point on a circle makes an angle of 90 degree with radius drawn at that point. Here since both circles are touching internally, so only one common tangent is possible.
Complete step-by-step answer:
The steps for making the required construction are as follow:
Step1: Draw a line segment of 3cm
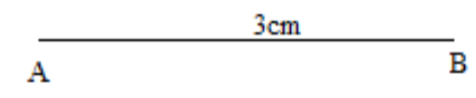
Step2: Then draw a circle of radius 5cm taking as the centre. The circle is drawn using a compass.

Step3: Now draw another circle of radius 2cm taking B as the centre. Since the distance between the centres is 3cm. So, both the circles will touch at the point P.

Step4: Now to draw the common tangent, we will make an angle of 90 degree at the common point of the two circles. So, we will join AP and then draw a perpendicular to AP at vertex P.
The perpendicular XX’ formed by joining the two points will be the required common tangent of two circles.

Note In the construction related to the tangent on the circle, the important point is that you should know that the tangent drawn at a point on a circle makes an angle of 90 degree with radius drawn at that point. Here since both circles are touching internally, so only one common tangent is possible.
Recently Updated Pages
Three beakers labelled as A B and C each containing 25 mL of water were taken A small amount of NaOH anhydrous CuSO4 and NaCl were added to the beakers A B and C respectively It was observed that there was an increase in the temperature of the solutions contained in beakers A and B whereas in case of beaker C the temperature of the solution falls Which one of the following statements isarecorrect i In beakers A and B exothermic process has occurred ii In beakers A and B endothermic process has occurred iii In beaker C exothermic process has occurred iv In beaker C endothermic process has occurred

The branch of science which deals with nature and natural class 10 physics CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Define absolute refractive index of a medium

Find out what do the algal bloom and redtides sign class 10 biology CBSE

Prove that the function fleft x right xn is continuous class 12 maths CBSE

Trending doubts
Assertion CNG is a better fuel than petrol Reason It class 11 chemistry CBSE

How does pressure exerted by solid and a fluid differ class 8 physics CBSE

Number of valence electrons in Chlorine ion are a 16 class 11 chemistry CBSE

What are agricultural practices? Define

What does CNG stand for and why is it considered to class 10 chemistry CBSE

The rate of evaporation depends on a Surface area b class 9 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

State whether the following statement is true or false class 11 physics CBSE

A night bird owl can see very well in the night but class 12 physics CBSE



