
Construct a $\Delta PQR$ whose perimeter is $12$ c.m. and the lengths of whose sides are in the ratio of $2:3:4$.
Answer
521.1k+ views
Hint : To draw a triangle, we will draw a line of length of its perimeter. Then, we will draw a ray from one point in a straight line. After that, we will divide the ray into $9\left( 2+3+4 \right)$ equal parts and will mark the points length of 2, then 3 and after that 4. We will join the last point of the ray to the other end of the straight line. Then, we will draw parallel lines to the mark point that will cut the straight line in two points. Then, we will draw a circle of radius of one end to the first cut of straight length. After that, we will draw another circle of radius of length of second cut to the other end of straight length. Then we will join the intersection point of circles to the cut point of the straight line to draw the required triangle.
Complete step-by-step solution:
Since, we have given the ratio of sides as:
$\Rightarrow 2:3:7$
The perimeter of the triangle$=12$
Draw a straight line first named AB.

Then, draw a ray down the side of the straight line with an acute angle and divide it in some equal points. Then, we will draw the length of $2$ AC, then the length of 3 CDs and after that the length of 4 DM.
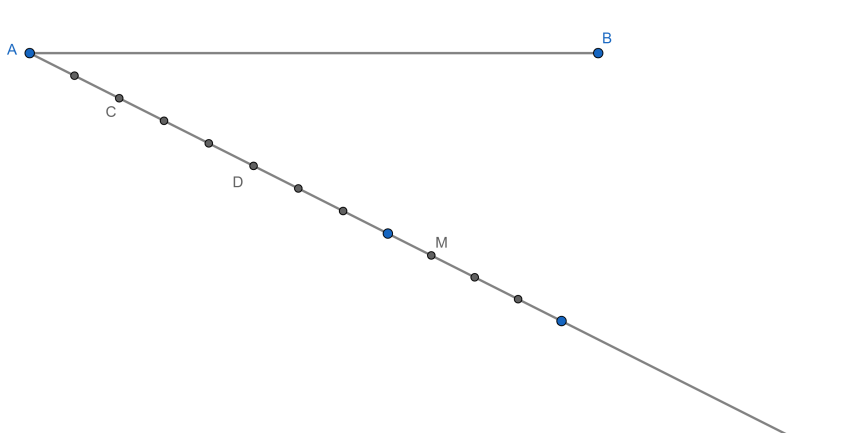
After that, we will join the line BM and draw the parallel line to BM at point C and point D that will intersect with the straight line.
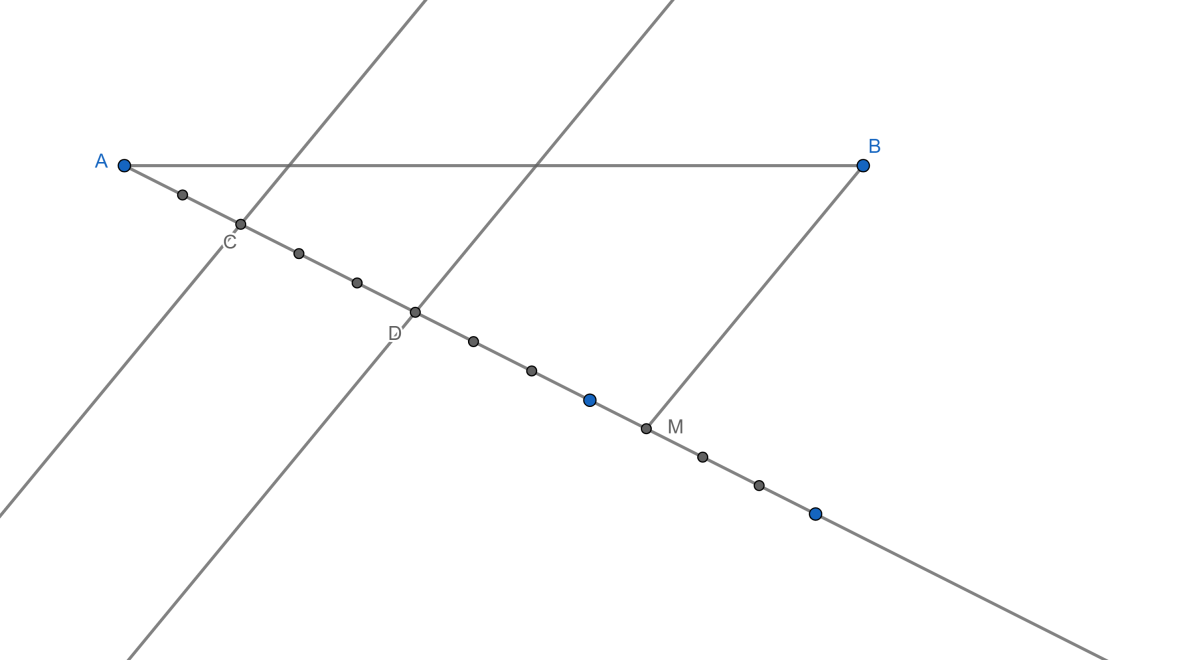
Then, we will draw a circle from point P at the length of AP and another circle at point R at a length of RB.
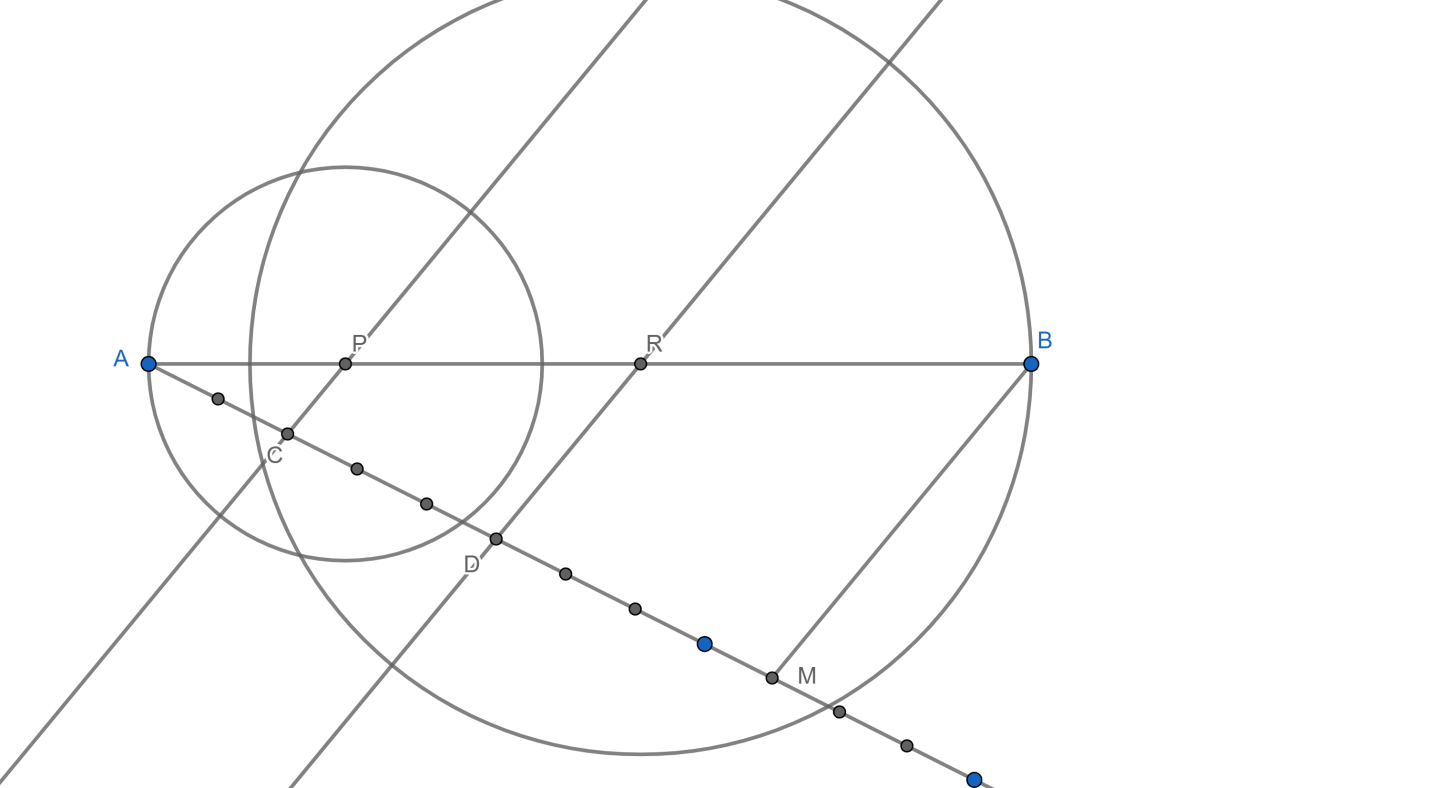
Then, we will join the intersection point of both circles to the point P and pint R as:
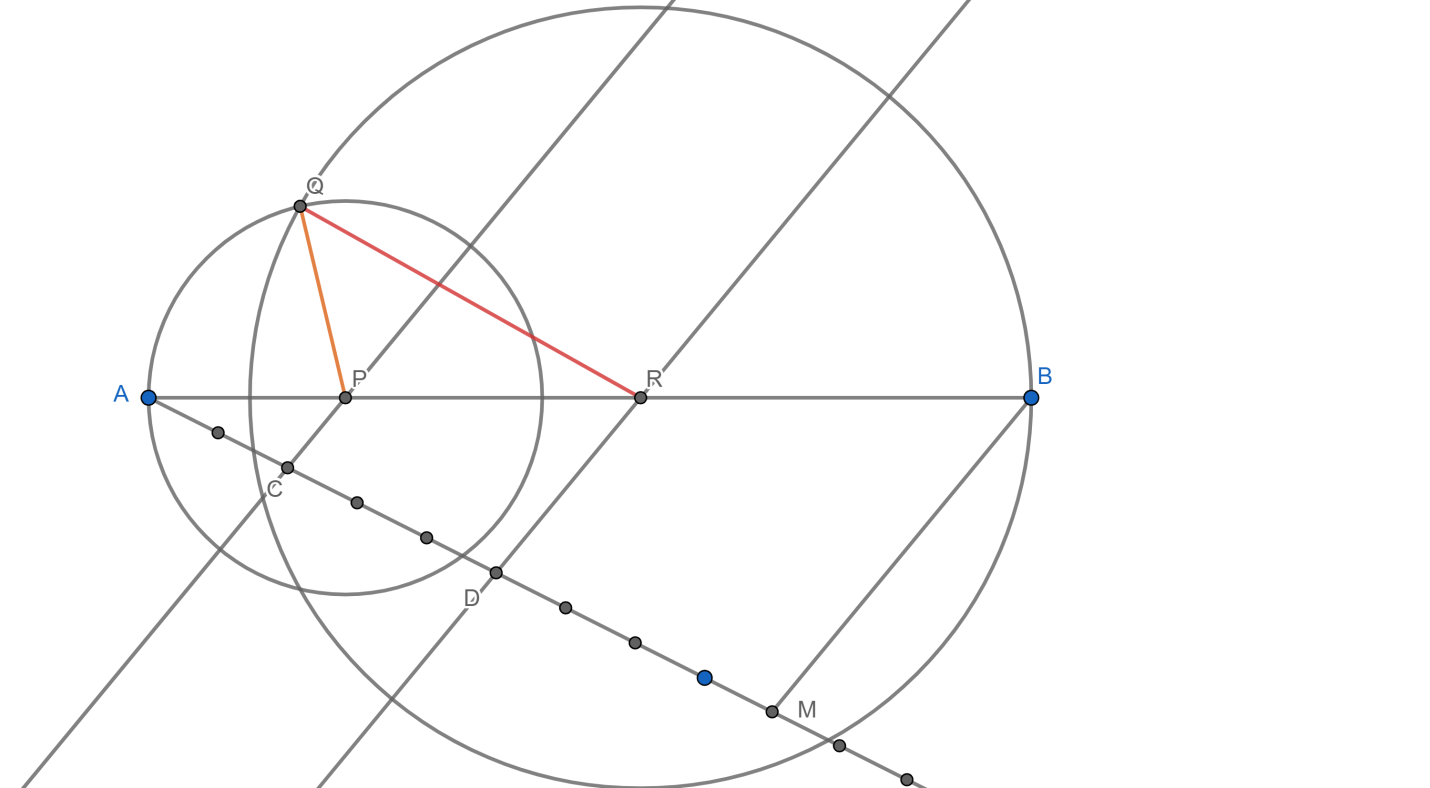
Hence, the required circle will be drawn.
Note: Triangle is a $2D$ diagram made by using three sides. It has three points, angle and vertex also. There are total six types of triangles based on its sides and angle mentioned below:
Complete step-by-step solution:
Since, we have given the ratio of sides as:
$\Rightarrow 2:3:7$
The perimeter of the triangle$=12$
Draw a straight line first named AB.

Then, draw a ray down the side of the straight line with an acute angle and divide it in some equal points. Then, we will draw the length of $2$ AC, then the length of 3 CDs and after that the length of 4 DM.

After that, we will join the line BM and draw the parallel line to BM at point C and point D that will intersect with the straight line.

Then, we will draw a circle from point P at the length of AP and another circle at point R at a length of RB.

Then, we will join the intersection point of both circles to the point P and pint R as:

Hence, the required circle will be drawn.
Note: Triangle is a $2D$ diagram made by using three sides. It has three points, angle and vertex also. There are total six types of triangles based on its sides and angle mentioned below:
| Based on angle: | Based on sides: |
| Right angle Triangle | Equilateral Triangle |
| Acute Triangle | Isosceles Triangle |
| Obtuse Triangle | Scalene Triangle. |
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Who Won 36 Oscar Awards? Record Holder Revealed

Why is there a time difference of about 5 hours between class 10 social science CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE




