
Construct a
Answer
487.2k+ views
Hint:
We start solving the problem by first drawing the line segment AB and then constructing the angle
Complete step by step answer:
According to the problem, we need to construct a
Let us first construct
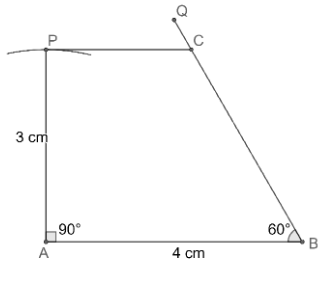
(i) Let us first draw the line segment AB of length 4 cm using a ruler.
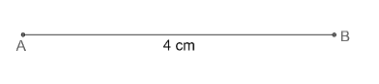
(ii) Now, let us construct the angle
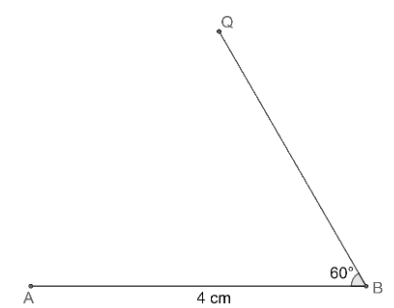
(c) Let us draw an arc of length 3 cm by taking A as a centre.
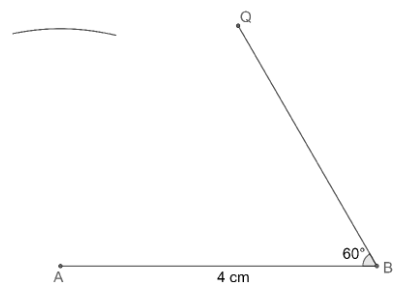
(d) Now, let us construct the angle
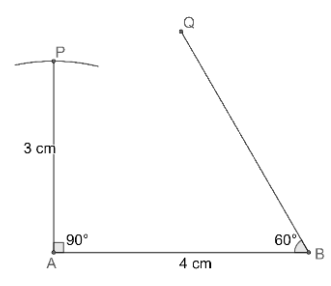
(e) Now, let us construct the angle
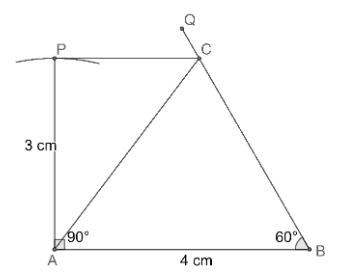
(f) Now, let us join the points A and C to complete
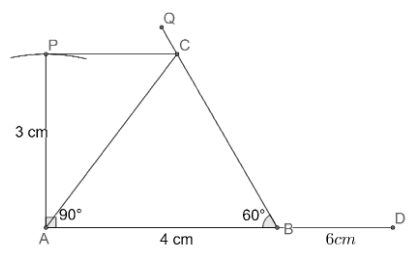
(g) Now, let us extend AB to D such that
(h) Now, let us construct the angle
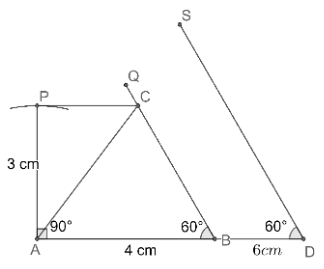
(i) Now, let us extend AC to intersect DS at E to complete
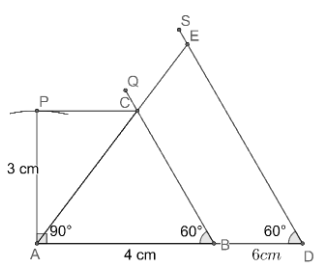
Note:
We can take the ratio of the sides of the triangles ABC and ADE to verify the similarity of both the triangles. We need to follow each step carefully in order to avoid confusion and mistakes in the diagram while constructing the triangles. Similarly, we can expect problems to draw the circum-center of the obtained triangle
We start solving the problem by first drawing the line segment AB and then constructing the angle
Complete step by step answer:
According to the problem, we need to construct a
Let us first construct
(i) Let us first draw the line segment AB of length 4 cm using a ruler.

(ii) Now, let us construct the angle

(c) Let us draw an arc of length 3 cm by taking A as a centre.

(d) Now, let us construct the angle

(e) Now, let us construct the angle

(f) Now, let us join the points A and C to complete

(g) Now, let us extend AB to D such that

(h) Now, let us construct the angle

(i) Now, let us extend AC to intersect DS at E to complete

Note:
We can take the ratio of the sides of the triangles ABC and ADE to verify the similarity of both the triangles. We need to follow each step carefully in order to avoid confusion and mistakes in the diagram while constructing the triangles. Similarly, we can expect problems to draw the circum-center of the obtained triangle
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Gautam Buddha was born in the year A581 BC B563 BC class 10 social science CBSE

Fill the blanks with proper collective nouns 1 A of class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




